2019 SBI PO/Clerk Quantitative Aptitude Short Cut Tricks Series-2

As promised, ixamBee is back with the next series of Quantitative Aptitude short cut tricks. In this article, let us look at short cut tricks of Boats and Streams Chapter, which is one of the most common topics in Quantitative Aptitude Section. It is related to Time, Speed and Distance and the concepts are easy to understand. It requires direct application of formulae to solve the questions. In all banking exams, at least there is 1 Q asked from Boat & Stream chapter.

Lets us first learn the terms used in Boats and Streams Topics:

Net speed of the boat is called downstream speed when the boat moving along the direction of the stream. 

Net speed of the boat is called upstream speed when the boat is moving in the direction opposite to the direction of the stream.

Let u = speed of the boat/ man in still water

& v = speed of the stream/ current / water / flow.

Then Net Downstream (in same direction of flow) speed = u + v

&Net Upstream (against the flow) speed = u  v

Trick 1:

If a boat or a man travels downstream from point A to point B & then returns upstream from point B to A,

Then its average speed during the journey =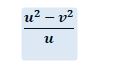 

Q 1. A boat takes 4 hours for traveling downstream from point A to point B and coming back to point A upstream. If the velocity of the stream is 2kmph and the speed of the boat in still water is 4kmph, what is the distance between A and B?

Solution: (6 km)

Here      u= 4kmph,

v = 2kmph

So average speed of boat during the journey = kmph

Here time taken by boat during the journey = 4 hours

So distance travelled by boat during the journey = speed × time = 3 × 4 = 12km

Hence, distance between A to B = 12/2 = 6km.

Q2. A man can row 5kmph in still water. If the river is running at 1kmph, it makes him 75minutes to row to a place and back. How far is the place in km?

Solution: (3 km)

Here      u = 5kmph,

v = 1kmph

So average speed of man during the journey =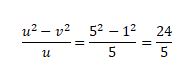   

Here time taken by man during the journey = 75 minutes = 75/60 hrs = 5/4 hrs

So the distance traveled by the man during the journey = speed × time =   ×  = 6km

Hence, the place is 6/2 = 3km far.

Q3. The current of the stream runs at 1kmph. A motor boat goes 35km upstream and back again to the starting point in 12hours. The speed of the motor boat in still water in kmph is.

Solution: (6 kmph )

Here v = 1kmph & distance covered by boat = 70 km

(35km upstream & 35km downstream)

Here time taken by boat during the journey = 12 hrs

So average speed of boat during the journey =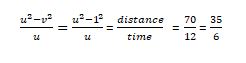  

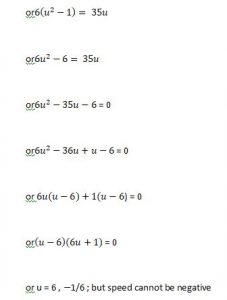
or u = 6 , 1/6 ; but speed cannot be negative

So speed of the boat = 6kmph.

Trick 2:

If time taken by a boat covering a certain distance in upstream = n times of time taken by boat covering same distance in downstream

i.e., then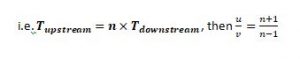 

Q4. A man can row 28/3 kmph in still water and finds that it takes him thrice as much time to row up than as to row down the same distance in theriver. The speed of the current in kmph is

Solution: (14/3 kmph)

Here, n = 3 &u =28 /3 kmph

As we know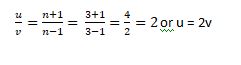 

or v = u/2 = (28/3)/2 = 14/3

Hence the speed of the current = 14/3 kmph

Q5. River is running at 2kmph. It takes a man twice as long to row up as to row down the river. The rate of the man in still water (in kmph) is

Solution: (6 kmph)

Here, n = 2 &v = 2 kmph

As we know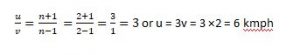  

or u = 3v = 3 ×2 = 6 kmph

Hence rate of the man in still water = 6 kmph

Q6. A man can row at the rate of 3 kmph in still water and he find that it takes him twice as much time to row up than as to row down the same distance in the river. The speed of the water in kmph is :

Solution : (1 kmph)

Here, n = 2  &  u = 3 kmph

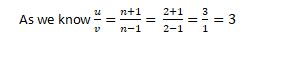
or  u = 3v  or v = u / 3 = 3/ 3 = 1 kmph.

Hence speed of the water  =1 kmph

Q7. A boat covers a certain distance downstream in 1 hour, while it comes back in 11⁄2hours. If the speed of the stream be 3 kmph, what is the speed of the boat in still water?

Solution : (15 kmph)

& v = 3 kmph

Hence speed of the boat in still water   = 15 kmph

Q8. A boat running upstream takes 8 hours 48 minutes to cover a certain distance, while it takes 4 hours to cover the same distance running downstream. What is the ratio between the speed of the boat and speed of the water current respectively?

Solution: (8:3 )

Hence the ratio between the speed of the boat and speed of the water current = 8:3

Practice Free Mock Tests for SBI Clerk Prelims

Practice free mock tests for SBI PO Prelims 

ixamBee has started Quantitative Aptitude Short Cut Tricks Series, this is the second blog in the series.

Read her the first blog:

2019 SBI PO/Clerk Quantitative Aptitude Short Cut Tricks Series-1

Stay Tuned & Practice hard for more tricks!!!!!!!!!

Get Free Online Test Series, Daily GK Update, PIB Current Affairs, Banking Awareness as well as latest updates for Bank PO, Bank Clerk, SSC, RBI, NABARD and Other Government Jobs. oneclick займзайм не в банкезайм под 0 %