Question
A and B together can complete a work in 6 days, B and C
together in 8 days, and C and A together in 12 days. In how many days can each of them complete the work alone?Solution
Let daily work rates be a, b, c. a + b = 1/6 b + c = 1/8 c + a = 1/12 Add all three: 2(a + b + c) = 1/6 + 1/8 + 1/12 LCM(6, 8, 12) = 24 1/6 = 4/24, 1/8 = 3/24, 1/12 = 2/24 So 2(a + b + c) = (4 + 3 + 2)/24 = 9/24 = 3/8 ⇒ a + b + c = 3/16 Now, a = (a + b + c) − (b + c) = 3/16 − 1/8 = 3/16 − 2/16 = 1/16 So A alone takes 16 days. b = (a + b + c) − (c + a) = 3/16 − 1/12 LCM(16,12) = 48 3/16 = 9/48, 1/12 = 4/48 ⇒ b = (9 − 4)/48 = 5/48 So B alone takes 48/5 days. c = (a + b + c) − (a + b) = 3/16 − 1/6 3/16 = 9/48, 1/6 = 8/48 ⇒ c = (9 − 8)/48 = 1/48 So C alone takes 48 days.
((9.77)0- 〖(0.1)〗(-1))/(〖(6/24 )〗(-1) ×(3/2)3+ 〖((-2)/6)〗(-1) ) = ?
...(23.95)2 – (25.006)2 + (8.0099)2 – (7.07)2 = ? - (14.990)2
√10404 + √9604 - ∛1728 - ∛42875 = ?
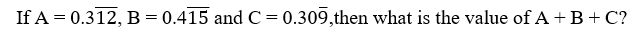
(144 ÷ 4)² × (72 ÷ 12)³ = 12 ×? × (25920 ÷10)
Simplify the following expression:
(3/5 of 250 + 40% of 150) ÷ (0.75 of 80)
What will come in place of the question mark (?) in the following expression?
46 – 5² + 8² + 3² = ? × 4
If (x + 1/x) = 5, then value of x3 + 1/x3 is:
What will come in place of the question mark (?) in the following question?
24.30% of 372.32 = ?
(? + 16) × 12 + 25% of 840 = 252 + 5



