Question
In AABC, P is a point on AB such that PB: AP = 3: 4 and
PQ is parallel to AC. If AR and QS are perpendicular to PC and QS = 9 cm, what is the length (in cm) of AR?Solution
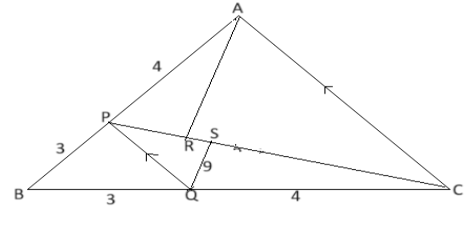△ ABC with P on AB such that PB: AP = 3: 4. PQ || AC. AR ⊥ PC and QS ⊥ PC. QS = 9 cm. Proportional Segments: Given – PB: AP= 3: 4, let PB = 3k and AP = 4k. Therefore, AB = PB + AP=3k =4k = 7k. Similar Triangles: Since PQ || AC, triangles △ APQ and △ APC are similar. This implies the ratio of their corresponding sides is. PB/AB=3/7 Area of △PBQ/△ABC =9/49 Ratio of △APC and △QPC- =½ ×PC×AR: ½×PC×QS =AR: QS △APC/△QPC =AR/QS           … (1) Area of △PBQ=9 and △QPC =12 Now Area of △APC =△ABC –(△PBQ+△QPC) =49-(9+12) =28. From Eq-(1) 28/12 =AR/9 AR =21cm.
During processing, foods can get contaminated because of:
a.   Equipments
b.   Labour
c.   Raw materials
Factors which affect internal corrosion of cans include:
Options:
1. Lacquer coating
2. Anthocyanins
3. Temperature
4. Acidic foods
The limiting amino acid in green vegetables is:
Toughening effect on canned beans is due to:
Rapid precooling method:
Probiotics are:
(i)Â Â Â Â Â Â Â Â Â Â Â saponification
(a)Â triglycerides
(ii)Â Â Â Â Â Â Â Â Â Â milk fat
(b)Â alkali
(iii)Â ...
In cryogenic freezing the liquid nitrogen temperature is:
In which of the following method, heating is due to electrical resistance of a food
Lakadong turmeric is famous for
Relevant for Exams:
