Question
Two circles with centers B and D have radii DA = 8 cm
and BC = x cm, respectively. AC is tangent to both circles. If DB and AC intersect the point E, AE = 12 cm, and EC = 18 cm, then find the value of x (in cm).Solution
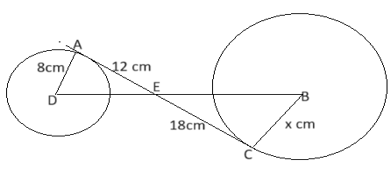AD ⊥ AC and BC ⊥ AC ∠DAE = ∠BCE = 90° In △ DAE and △ BCE ∠DAE = ∠BCE = 90° ∠AED = ∠BEC (Vertical angle) △ DAE ~ △ BCE (By AA similarity) By C.P.C.T = AE/EC = AD/BC = 12/18 = 8/BC  BC = (18×8)/12 =144/12 x= 12cm  The correct answer is 12 cm.
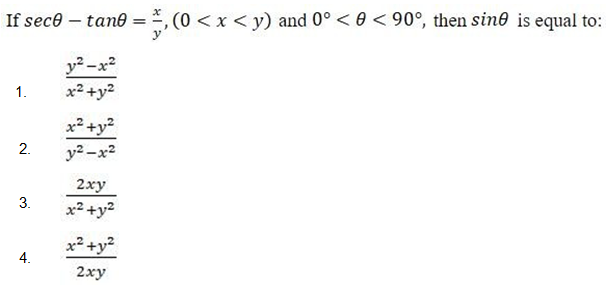
If a + b + c = 12 and ab + bc + ca = 47, and a, b, c are real numbers, find the value of a³ + b³ + c³ − 3abc.
If a + `1/b` = 1 and b + `1/c` =1 , then the value of c + `1/a` is
A sum of Rs. 25,000 is invested in SIP 'G' which offers 7% p.a. simple interest for 7 years. The interest received from SIP 'G' is invested in SIP 'H' w...
If
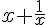= 2 then find In a best-of-two chess match between Player X and Player Y, the probability that Player X wins a game is (5/9), and the probability that Player Y loses ...
If 10x2 – 6xy+y² – 4x+4= 0, then find the value of (3x+2y).
If x 2  – 15x + 51 = 0, then determine the value of (x – 5) + {1/(x – 5)}.
For a =-4 and b = 5, value of a² – b² is:
Relevant for Exams:
