Question
The secant CD intersects the circle at E and CF is tangent to the circle at F. If the length of the secant CD is equal to 20 cm and the length of tangent CF is 15 cm, find the length of the chord DE.
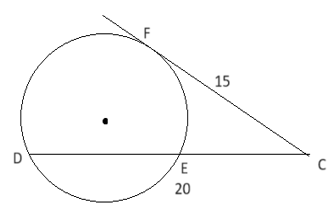CF is the tangent segment, which is 15 cm. CD is the secant segment, which is 20 cm. DE is the chord we want to find. According to the Power of a Point theorem: CF2 = CD × CE Since CD = CE + ED and CE =CD-DE, we can rewrite the equation as 152 = 20 × (20- DE) Now, 225 /20=20-DE 11.25 =20-DE DE =20-11.25 =8.75 The length of the chord DE is 8.75cm,More Mensuration Questions
- The circumference of a circle is 55 cm and the length of the rectangle is 8 times the radius of the circle. Find the area (in cm2) of the rectangle, if the...
- If the curved surface area and the radius of a cylinder are 880 cm2 and 28 cm, respectively, then find the volume (in cm3) of the cylinder.
- A closed wooden box of uniform thickness has length, breadth and height 20cms, 16cms and 12 cms respectively. If the thickness of the wooden block is 2 cms...
- A rectangular hall is 24 m long and 15 m wide. Find its area and the cost of flooring it at Rs 45 per square metre.
- The dimensions of a cuboidal box are in the ratio 3:2:1. If the total volume of the box is 546.75 cm³, determine its lateral surface area.
- The ratio of the length to breadth of a rectangular playground is 7:5. If the cost of fencing the playground at the rate of Rs. 4 per metre is Rs. 1920, th...
- The perimeter of a sector of a circle, whose radius is 22 cm, is 64 cm. If the length of a rectangle is 10 cm more than the arc subtended by the sector and...
- The radius of a cylinder is the same as the radius of a circle whose circumference is 176 units. If the height of the cylinder is 25% more than its radius,...
- Which of the following numbers is a divisor of (4915 – 1)?
- The length of a rectangle is 18 cm more than the side of a square. The perimeter of the square is 72 cm. If the breadth of the rectangle is 12 cm less than...
Relevant for Exams:
Hey! Ask a query
Please enter email id
The email must be a valid email address.
Please enter Mobile Number
Please enter valid Mobile Number
Please enter your Doubt
Think You're Ready for RBI Grade B?
RBI Grade B 2026 Phase 1 Memory Based Paper
- 200 Questions with Detailed Solutions
- Section-wise Coverage (GA, English, Quant & Reasoning)