Question
Given that 'θ' is an angle less than 120 °
, what is the value of 'θ' if it satisfies the equation 3cos 2 θ = 2 + sin 2 θ.Solution
Given, 3cos 2 θ = 2 + sin 2 θ
3cos 2 θ - sin 2  θ = 2
3cos 2 θ - (1 - cos 2  θ) = 2
4cos 2 θ = 3
cos 2 θ = (3/4)
cosθ = √3/2 (Since, in options maximum value of 'θ' is 90 o  therefore, we will take the positive root only)
cosθ = cos30 o
θ = 30 o
More Trigonometry Questions
If (sin 3A sec 6A = 1) , then what will be the value of cos 6A?
What is the value of cosec30° sec30°?
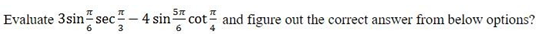
- Determine the value of:(sin 38 o cos 52 o  + cos 2  38 o ) X sin 30 o  + (cos 60 o tan...
- If 2cosec 2  A – cot 2 A = 5 and 0 o < A < 90 o , then find the value of ‘A’.
Find the maximum value of 14 sin A + 24 cos A.
If sin A - cos A = 3/7, then find value of sinA + cos B, where A is an acute angle.
If 4sin² θ = 3(1+ cos θ), 0° < θ < 90°, then what is the value of (2tan θ + 4sinθ - secθ)?
If tan θ + cot θ = 2 where 0 < θ < 90 ; find the value of tan17 θ + cot19 θ.
Relevant for Exams:
