Question
If 4sin² θ = 3(1+ cos θ), 0° <
θ < 90°, then what is the value of (2tan θ + 4sinθ - secθ)?Solution
4 (1 - cos2 θ) = 3 + 3cos θ ⇒ 4 - 4cos2 θ = 3 + 3cos θ ⇒ 4cos2 θ + 3cos θ - 1 = 0 ⇒ 4cos2 θ + 4cos θ - cos θ - 1 = 0 ⇒ 4cos θ (cos θ + 1) - 1 (cos θ + 1) = 0 ⇒ (4cos θ - 1) (cos θ + 1) = 0 ⇒ cos θ + 1 = 0 ⇒ cos θ = - 1 [Not possible because 0° < θ < 90] ⇒ 4cos θ - 1 = 0 ⇒ cos θ = 1/4 We can get all value by using the image below,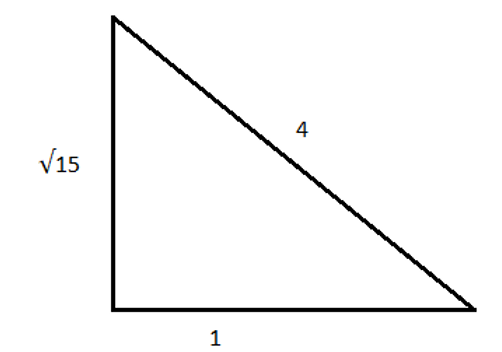 
The height will be = √(42 - 12) = √(16 - 1) = √15 So, (2tan θ + 4sin θ - sec θ) = (2 × √15) + (4 × √15/4) - 4 = 2√15 + √15 - 4 = 3√15 - 4
Which city in Uttar Pradesh is known for the ancient Dashashwamedh Ghat?
 Bandhan bank has roped _________ as its brand ambassador for the bank’s product and service endorsement.
What state ranked as the top electronics exporter in India during the fiscal year 2022-2023?
How many other levels does the idea of people’s participation in the Panchayati Raj System extend to?
Who has been appointed as the woman president of Table Tennis Federation of India for the first time?
What is Tripitaka?
'Man -Yi' a super typhoon has hit which of these countries recently?
Number of bones in adult human body are?
Kanger Valley National Park, which was seen in the news, is in which state?
Which day is celebrated as 'World Earth Day'?
Relevant for Exams:
