Question
If sin⁶ x + cos⁶ x = 7/8, find sin⁴ x +
cos⁴ x:Solution
We know that: sin⁶ x + cos⁶ x = (sin² x + cos² x)(sin⁴ x + cos⁴ x - sin² x cos² x). Since sin² x + cos² x = 1, We get: 1 × (sin⁴ x + cos⁴ x - sin² x cos² x) = 7/8. Now, let sin² x cos² x = z. So, sin⁴ x + cos⁴ x = 1 - 2z. From the equation 1 - 2z –z = 7/8, solving gives: 3z = 1 - 7/8 = 1/8, hence z = 1/24. Thus, sin⁴ x + cos⁴ x = 1 - 2 × 1/24 = 1 - 1/12 = 11/12. Correct option: c) 11/12
- If the number '6k3942' is divisible by 3, then find the maximum value of 'k'.
There are 8 classrooms, each with an average of 16 students. No classroom has the same number of students, and all classrooms, except the 8th one, have ...
- A number when divided by 221 gives a remainder 13. What will be the remainder when the same number is divided by 13?
- What is the remainder when
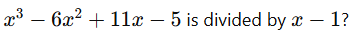
Find the number of zeroes in the product of 60 × 61 × 62 × ........ × 80?
The difference between the value of the number increased by 20% and the value of the number decreased by 30% is 120. Find the number.
- If the 4-digit number p89q is exactly divisible by 9, what is the least value of (p + q)?
If 94*6714 is divisible by 11, where * is a digit, then * is equal to
When a number is divided by 29 remainder is 18. Find the remainder when eight times of the same number is divided by 29.
The difference between the squares of two positive numbers is 18 times the difference between the numbers. If the smaller number is 7, then what is the ...



