Question
The height of a solid cylinder is 30 cm and the diameter
of its base is 10 cm. Two identical conical holes each of radius 5 cm and height 12 cm are drilled out. What is the surface area (in cm²) of the remaining solid?Solution
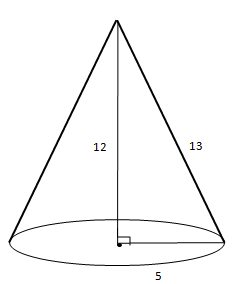
According to question: Height of cylinder = 30 cm Radius of cylinder = 5 cm Height of cone = 12 cm Radius of cone = 5 cm We know that, l2 = h2 + r2 ⇒ l2 = 122 + 52 ⇒ l2 = 144 + 25 ⇒ l = 13 cm The surface area of the remaining figure = surface area of cylinder + 2 × surface area of the cone ⇒ 2πrh + 2πrl ⇒ 2πr(h + l) ⇒ 2π × 5(30 + 13) ⇒ 430π ∴ The surface area of the remaining solid is 430π. 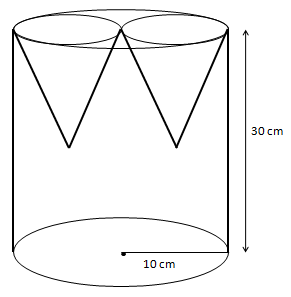
निम्लिखित में से शुद्ध शब्द छाँटिए
राजू अपने सभी मित्रों के साथ मंदिर गया था।
निम्नलिखित प्रश्नों में दिये गये पांच विकल्पों में से शु�...
निम्नलिखित प्रश्नों में दिये गये पांच विकल्पों में से शु�...
निम्नलिखित में से कौन सा वाक्य शुद्ध है?
अरब सागर में स्थित लक्ष्यद्वीप प्रवाल भित्ति से निर्मित �...
कृपा ( 1) / करें ( 2) / हे प्रभु , (3) / मुझ पर ( 4) वाक्य संरचना का सह�...
निम्नलिखित में से कौन सा वाक्य शुद्ध है ?
'जो लुप्त हो गया हो' के लिए एक शब्द क्या होगा ?
निम्न लिखित प्रत्येक प्रश्न को चार भागों में बांटा गय�...
Relevant for Exams:


