Question
How many distinct arrangements of DAUGHTER are there if
the vowels remain together?Solution
ATQ, Vowels = A, U, E Consonants = D, G, H, T, R (all distinct) Items = 1 (vowel block) + 5 = 6 (all distinct) Arrangements = 6! = 720 Arrangements of vowels = 3! = 6 Total words = 720 × 6 = 4320
More Permutation and combination Questions
(12% of 1250 + 85% of 400) x 10 = ?2
1/6+ 999*53/54 ×9 = ?
(49 x ?) / 3.5 + 389 = 627
What value should come in place of the question mark (?) in the following question?
20% of 1500 – 75% of 200 = 125% of ?
Solve the following:
1500 ÷ (9 × 18 ÷ 6 × 3 – 45) ²
- Which of the following expressions are equal?
'A' = 81 ÷ 9 × 6 - 27
'B' = (3/2) × (40/3) + 30 ÷ 6
'C' = (40 + 12 - 22) ÷ 6 × 5 Find the simplified value of the given expression
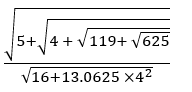
1111.25 × 9.05 + 2323.23 × 9.05 – 2121.37 ×9.05 =?
Find the value of x.
 √441 ÷ 21+ √400 = 1 × x
- Determine the value of ‘p’ if p% of 600 + {1440 ÷ p of 16} × 8 = 156
Relevant for Exams:
