Question
Which of the following statements is true?
Read the following information carefully and answer the questions given below it: P, Q, R, S, T, U, V and W are sitting around a square table in such a way that four of them who sits at the corner are facing towards the centre and other four who sits in the middle of the table are facing outside the centre. Each person has different number of coins viz. 1, 2, 3, 4, 5, 6, 7 and 8, but not necessarily in the same order. Only one person sits between W and V. V sits second to the right of the person who has 8 coins. W’s brother S, sits on the immediate left of his mother who has 6 coin. P is the father of V and only one person sits between W’s mother and T. S’s daughter sits second to the right of U and on the immediate left of that person who has 3 coins. Q sits second to the left of W’s husband who has neither 4 nor 7 coins. U, who is sister of V, has 7 coins and is not an immediate neighbour of W’s husband. T sits on the immediate right of the person who has 2 coins. S’s daughter has 1 coin. Only one person is sitting between P and U. No female is an immediate neighbour of Q, who sits at the corner of the table. V is father of R and is not an immediate neighbour of T. P is married to W.Solution
W’s brother S, sits on the immediate left of his mother who has 6 coins. P is the father of V and only one person sits between W’s mother and T. U, who is sister of V, has 7 coins and is not an immediate neighbour of W’s husband. V is father of R and is not an immediate neighbour of T. P is married to W. By the statement ‘only one person sits between W’s mother and T’, we find that Q is W’s mother and T is S’ daughter. 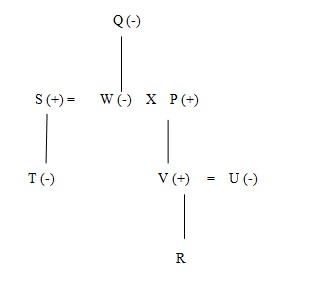 No female is an immediate neighbour of Q, who sits at the corner of the table. Q sits second to the left of W’s husband who has neither 4 nor 7 coins. Only one person is sitting between P and U. S’s daughter sits second to the right of U and on the immediate left of that person who has 3 coins. T sits on the immediate right of the person who has 2 coins.
No female is an immediate neighbour of Q, who sits at the corner of the table. Q sits second to the left of W’s husband who has neither 4 nor 7 coins. Only one person is sitting between P and U. S’s daughter sits second to the right of U and on the immediate left of that person who has 3 coins. T sits on the immediate right of the person who has 2 coins. 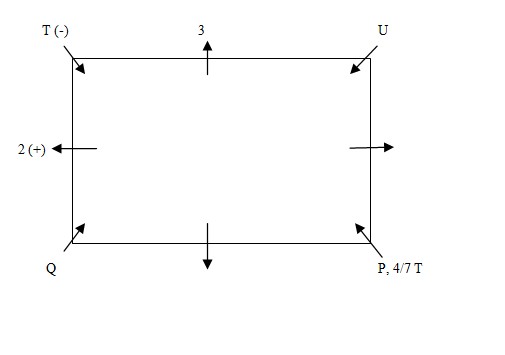 S, sits on the immediate left of his mother who has 6 coins. V is not an immediate neighbour of T. So, V can sit at immediate right or immediate left to P. If V sits immediate right to P, and as we know that W is female so she sit at immediate left to T. We know that V sits second to the right of the person who has 8 coins. By this statement this condition is not possible. If V sits immediate left to P, so W will sit at immediate right to P. Then R will sit at immediate left to T. Further V sits second to the right of the person who has 8 coins. It is given that T has 1 coin and that of U is 7. So V will have 4 and P will have 5 coins
S, sits on the immediate left of his mother who has 6 coins. V is not an immediate neighbour of T. So, V can sit at immediate right or immediate left to P. If V sits immediate right to P, and as we know that W is female so she sit at immediate left to T. We know that V sits second to the right of the person who has 8 coins. By this statement this condition is not possible. If V sits immediate left to P, so W will sit at immediate right to P. Then R will sit at immediate left to T. Further V sits second to the right of the person who has 8 coins. It is given that T has 1 coin and that of U is 7. So V will have 4 and P will have 5 coins 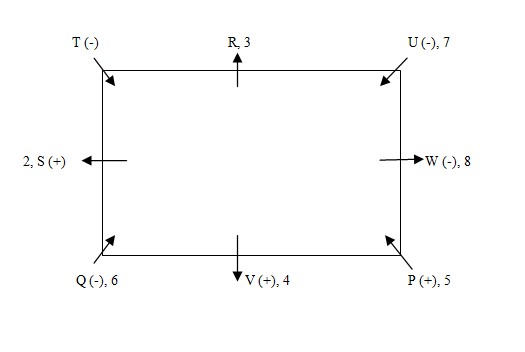
Which of these famous footballer has announced his retirement from the game on 3rd November, 2022?
During which military conflict did the Indian Army launch "Operation Meghdoot" to secure control over the Siachen Glacier region?
Which government scheme has a component called "Recognition of Prior Learning (RPL)"?
Who will be receiving the 52nd Dadasaheb Phalke Award for the year 2020?
The Cabinet Committee on Economic Affairs has given its approval for the Minimum Support Prices (MSPs) for copra for 2024 season. Which of the following...
RBI proposed the Financial Inclusion Index (FI-Index) to capture the extent of financial inclusion across the country, it is based on three parameters: ...
Who was the first Governor of Uttar Pradesh?
When is International Dog Day celebrated across the globe?
How long the Non-cooperation Movement was conducted?
What is the premium amount for the ‘Snehamitram’ life insurance scheme for dairy farmers in Kerala?



