Question
Simplify the following expression:
src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAPIAAAArCAYAAABCWdVDAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAAEnQAABJ0Ad5mH3gAAB+8SURBVHhe7Z13XNVV/8Dfd7GXDAcCAuYATXHmypUjV+6y0sxMy7Jh48mm+lQ+lmU7s5xZrsxtOSIcKAIq4kBQQIaCwGVe4O7v+f3hgssFHBd8nn6+X6/7B9/POd9xzudz1udzDjIhhOAe97jH/zRyywv3uMc9/ve4Z8j3uMc/gHuGfI97/AO4Z8j3uMc/AFmti13CTFHuJbLzS5EqJRUIowt+IX642yuRVZDUK6Zy1JkZ5JbJcfcPoqm7yjJFPSLQ5GaQlammTCbDuUFD/Pz9cFZaprs7mDS5ZF3MJr/UgMLFB79m/ng6KSyT2QTJVE5uehq5heWY7RzwbtIMXx9X6uZpN4+xJIe0Mnv8vN1wVN29fkwylJGXq6Zc6UlgY9er9mNGV5rPxdQcdAo5cpkMQ3kxaWcS0DYKY9zDnahOu2s3ZF0+qz6cyvvLIykuNyGTAchQ2QnKfWeya9ub9ApwvwuGLMhPOUH4ngMk5xfj4BVMh0Gj6NfcxTJhvWAsyWbvzl/Yn1JMI2FPUdlljp67TEC/WSx4oQceinpWGgEVK6X45F6Wbz5IWrmCAGcNSefzkQX0ZfKMcfTwc66Y884w68lKPMSvO/5ArXfFS5i4mJXAsQI/psx8h2f7NLLMUS+I4nQi9uxi146N7PCYzNp/jaF9U6eqBVUvGEg58AvvLtyCvutrbHy/79UGTkPC/h+Z8fAc4hwUyAWYjXJcvDvwyldfMntUO8sbXad27TKUUyBcGD/jHT5Z+Bmff76IrxfPY2Sj++j9+AD8G7jUezEAXIrbxOIv/0O01JCHnpjCkxOG09XfyTKZzTEbLrNz7kQmTnycsaNHMWbs6+zOAX1eMus3H8I9bDDjpz/HjJmzmNBesO2rL9ifZcRseaO65Kpunt+8i9g9CRQVJrJm8Vpiiz0Z9OKLTHv5X8wc3ZbCI4v5dvkWLkuWN7gD9CUkx+xhaYSOgZOnMeWFmcx4ZjIdNb/x43frSTOBPjuKFb8ewpaPrZGCfSxZvoUCBxnm1HQuXipCb77Wf8nIifyR154dx7CR4xg/bizfbDtOrt7iHjZEnXSWrat3En0qHXVJxQeZMJkNeDfryCsffseXiz7niy8/Z+EnbzK8S7MK6awgasNkEHk5l0RBcZnQ6nRCbzQLffJOMfKRmWLTuWyht0xfH2RHii+fHy6GPr1AnNBYCusSSRjKEsWn3VWiVffpYvPRJHH2bKooMAhh1mnEhdQLQl1uuJ46ce2zwksVKr49Uy6MUqUb1TkZuxaK595YJDbEFYrsg8vEyJFTxNyfD99IUHZCfDX9IdGx/3Sx9Zy2YtY7w2wUGvUlkZByQzfMJRni50nOommHl8VxrRBSSaYIn/+IGPfJIWG0yF4nGItEdlau0IoU8dMjXUTD8d+I6IzS62JDcba4cOGCOP3H16J/qJcY++Fmcb6O9ErSZYqI9QvEi0OHiaH9hoher/8pTNelBeLU/s/ESyNeEscKhRDCLMwmkzAajMJkrlmBau+RFSq8G/rSwM0JB3t77JQSsX/vp2GnXnTxccfOMn2do+Xorp3sPiOjVZ++eKaf4Miho5xJykVnskxre4SQMBmMoPLgvjYtad06iAYqkNu7EBgUiJfjlVlMSdpxdu8rJmjSTEb6q1DW47ClMCGcH44UEtavB6PCPNCVl6NDhbNzhRGLU1MCmjTGIfsy2TkFFbPfGXIlLl6+hAQ3vqIb2kISD+1ld2oHBk17gnYOIHNtQqcJzxN05it+i86zvIPtUbrTuIkPDrhhr1Igk8mujFquonJrTGBgIG1a+uOokjCYzNQy4bxtzsdGEn4ildCxw2juASbJ4kFCQl9aSHrCOY5Gx3AqMZkyIUMhr1mBajdkC3SZh9kRp6Fnz/Z4OjtYiuue4lSij0UTX1yMriSV2OgIInasYtGnc1i8OZpyy/Q2R4ZMBjIEJqOlDC4dXsEnb7/Fc1Pf5u/8ML6Y+yR+rvW42mW8yJ4dB8E5hD5d26ECGjTxozHpHDkVy4WryQrTYjgQF0+uoyN2yltWg1oxlOZzaPX7zJrxKq+9tx2vkXNYMOOBq3NBBa4BfRj7cDv2rV1JUrGVgqwTRI0GKkxmBLI6myqWnt5B+C97MYdMZXB3f5BMgKyCESpB7kSRJovDMfs5EPEnq76ezYefrSO5ljK65RqMXv8VybomhLRsgoOqrj65evSFeWRll+DRuBU9+zxIz6HjmTR9DJ2aFrN38QrCk0ots9Qrjt5BhHbtyoMDg1Hn7OGLpQcpqL/ZIFmxf3HsQgnN27Qn0NsRAPeWfXj+0UG4HPqFp3oPZdyzH/HL5jSQXPHx9sDHq4Hlbe4YudIOn+bt6dqvMyFtyti1cyU/70y9IZc70Kr7QzQsOsim/RmV8v4jKT7LpoiDnGg6jA8mdSXY3RGl0g6lUkGZKYeTp0+jMbsS0PphZn78Hk+OfJjxEyYyrF9P8o4s5+c/42vUolszZO0BVm06T/NufQj2dr3FzLbBZDZi0Mvx9goktI0fjRr74RfUi67tQnBQx3PqzMWKo6Y6oabmy7N5dwYMGcpTL7zPmyN8OPjTS6w8osNYUy3YjHz2/r6XLKMXrUKCuGLGgH0DujwymfcXfMKH77/By89NYFiXRihkxcg9PWnibV/5NjZA6eBKcOdhjHpsCrPeeotxrttZ8sV8YvKvJpDJcW3cmod6BPHnxo0UWuT/RyGVceLAHpau2MBvKz9mzNAh9Bv7Gr8diOLkr68wYuQ01kWmIsnAzac5Dw7qR1iQP/6BLej8QB+CPPVEHj+LvgYduiVbPPTFG5xV9WdA//tp4HhLWW2GncoOlZ0CndmI6fpSsBKlozMOrvbYOznUaGh1hVlfSlp6FlqZPY4Ojri4+dK/W2ecyi4Qk1SAuYZKsBkZO4lO1+LbsRutAyq74RQuXjTv+AB9B/and5f7MOedILGsEWEPjaKNLTtkyYQmP5vEjGKUdo44OrgQcF8nhnUJJCf1BCm5N5Iq7F1o/0A37BM38cnhmoeOtkIOILsyPao3ZCoCOg5j/qKf+PWbfzPzpReZ9uRw7g9uRpOuj/Lm228x8eHuOJl0FGWnkll4Y7FHoXLEwU6O0WCqcVpw09ZoSN3AJ9/m03nyBMKaedw1x76qcQs6hAVhOHeAv8IvXbkoTpMQFU6uQ2vahDa1zFIPCHQ5Z/n+k3f4fv/Z61dPH79ArqIN3Vq7UB9u5IRNu0nVe9I6LAQvi+dVVILUPev5ZnMKXg9OYeqIrth0pcNQQmLESl569z8cLL5yyZibTuTRMhx9O9OiohtZJselWSjd3TWs+HwnmgqiusEegxzMpXrkTjb0ndeGzA7PpvfRq+8AhgwdxtAhw3ls1ADaNPTBs1F3hvbqSWigDxScZ9+qd/hg6XauDVyyz+7jaEI5bUOaY1+D0d2kepWxb8kytruOYNyAULzvwtz4OnZNGPDUC7wwJIDDnz7D8AlPMGXKHA5r2/PEqy/Rza+62Je6RIbKrgEt3WHnTy8yeuKTPDZlIouOG5kxfz7j7nejDtaTKiMls35/PHqfFrQO9LWUIpNB8l/LmP/GVL6PyaTN8Gd45ZmRhNk6PkPugLeHH03Lj/Dei0MZP2kSj8/5jNMNR/HRR6/SxrNSYhTO/vTpdR+54VtIqjOvQzF7N3zGu69P4vO/YlDv+YbZ0ybw4VfrOJ9RVOdTMUvK88+x4aflbNi+h6NbvubrbQnoAZW9M252EglbP2DyU48y4anHeWvTIYKGPs/U4R1q7Dxrj+wCQM+FyH0cklowpnsgTncxtO0KgtLsJI7HxJNapMfJtQHNQjrStmVTnGv62jtGYChL4ou+Iax0epO1Oz4lzPWqyGSiOCuFY+fjyb5sRNjb4eXXkk4d2tKwpqbUVqRtY+SYudiPeo/P3hlDgJWFcvW5I8SnZGPXrB33Nw/Cw74O6lEIzKXFZFw4RVxqKmXlKlQeDQhu3p72rXypMhs3G8j98wMajVzNwsPneOOBuugpdZw7EcW5jGyKNRKSJFCplHj6tqZju9Z4e1xZTRBJvzP8sekoR/3IZ6+PpcW1urUxhtJckuLiOJWcDY6eBIV0pnN7X1SSAU32eeLOnCGrUI9JqHBu6k9YSBiB3s41TxktHcv3qAlJ6EvPigWdEa17vyniSizld48L2z8SXQIHi9eXHxZWX6vmeIK7h2QU5QnLRSgyMXbJaUtpvSIlbhRD23uKR+ZsFOesFmIdIt1ZBdVBk1w7NY4BapLdoxoMXL6QTZHMHU8vN6wGqtbYnNdETRUiapTeFDIZskaNaQPknDpHkaX8v4jKemsZyFHtHzfHHa6+3RVDlsmMJEZFcjQ1r2oAhwwK085y5HQqGXUY72qd26iA/wq0FBWWUtbIiwbutthhJJGTlkjUkZPkWmkBjGVqTsQcJV5ji+AJOXIHHwKbCAyZ+dzdKICakclMJMUcJvbsRcosv1wGRRlJxBxPIF1/56Vyq9wVQwYZ5cm/s+rzj9kUmYaugkSTEcOKZT+x/dQ5DFUmVLZHmEo5G/ULsz9cREJR/VdAdUilqSxe9AHLDmRSZLCUWqKnVKel3NkJR3tbBM3KMKmPEr5qHt+tjqKwguvMqMlk19olLPljP6U2ms7KcMMnALRlOZTWjxfqNpGhTd7Mum8+ZuOBC1X0duXSJfx2PBF9PeitJXfJkJW06fcw97tmsO+Xb9gRlYoEaLPiWP/Das4UO9O5fUtq2e9hG8wG1JdOExEZjbpizdxlhKGIY9EHiM8oQVfb1imjngJtOSgVqJRWVrluGRmNW4TRrUNDLv3xFat+P3QlYEOfw99rV7JjfwYtuvegg020R4ZM7o5PYzAai9BpLeX/TSgI6TOItt75HFzzLdujUjEDZVknWL9kNScLnOj8QBhBltnqAZtUxS0jwN5vMJNefYM+fmr+WreCNdvWsPS7FRzL8mL0xGcYHhpc7SZqWyKz96Tn8Fms+PYTejW2lN49FJ4dmbNgCbNHt6Hx9RCtajAZKdFrcXNzwcXRNl5hhXtb+k96m4lDAkjes4wly9ew8dcf2fznJcJGPMOzg7tbn4vfBjKZM+6eAPI7nSpW4qYcMreCAPumA3lsxuv0DSggfN1yVvy+llU/ruL4JS9GPfUsY++vW72t7puquJ/mzJmD0Xj74xuDwUDfvn3p168fzs61j72MhdEs/3gxK7Zuxb7dZF6d9S6P9PKxOs8rLCxk165dHDt2DDu7qkNIk8lEcHAw48ePx8vLy1J8BW0BCZGbWLr7HA52SkCGXKHCTinDaNBhFjJAhkvDAAY/OpVOvhV7OOvuJ51Ox7x5867sqrGCJEl06tSJ0aNHo6ymx5TUiaz9fQeJGQWYBMhk8ivfaDZgNEkIwGzQ4tf3aR7t145GzhWepU1l4WvT+Vn7MJ+9+xKDW9wY22k0GrZs2UJ8fLzVMjMajbRq1YoRI0bQqFFVp7LQp/P3mh9ZuHANuT6BTHj2R16a1OJG+GcF9Ho9hw8fZufOnVafJYTA0dGRSZMmERR0o98y6zVsfd6Ndy/8i3XbP6G9hdun+MQGFv4Wb3FCTQWEQO7cgP5jn+HBVt5U9I5u2LCBU6dOYTKZrNZPeXk5L7/8MsHBwbfkfjIUxrBy/vcs3bQLl45jefGluYzu7WO1ZywoKGDXrl0cP37carncDGazmcaNGzNr1ixLEVjrkfPz81Gr1Xf0Ky0trbblsMSME5jkqMp0qJRGJEeqDQ6XJAmNRkNeXl6VZ6rVavLy8iguLsZsrmEsKiQM5cXk5VXMm0eeOo889dVvz1dTUFSE3nRz3yCEqPIulj+NRlNzmZgNlBQXos5Xk38tX17elffMv/F3UZm+arinTI5KoUBdXEKptvL8QJIkSkpKqrxPxV9JSQkmk/VoDAl7hGSPUqvDzmQAF1Ft/Qgh0Gq11daPWq2moKCg6rOEhNkE1a2CS/rSG2Vg7ZevJj+/EK2h6vZDjUZDfn5+tXqdl5eHwVDrIkQVJOEIZgV2ZTpUchPCsfpyMZvNaDSaKs++1V9RUfVr+lV65PpEr45n3bffsTvFjSEDgsiNiyS+JIjxz89gSFd/rPdddYCk4WKuHr/G3pYSC6z3yHVFYV4Wck9f3K0NTypizmLV7Bd5/lggi+e/xdPdbDNHEPrLHNjwIz9vO49/1+7cb5/Exr1qej3zOk+P7IhzlW7g9jBpL7JsjD9f695l3R8fcb+17v42EEJY7YWr42Z7ZG3eSX5b/D27zzvTu3dzdOeiOJ7vz9jnZzC8q3/V3tGGVPdNdfnMGjEVRPP7ks+JSFUwePIzTJj8ItNenUmY62W2LV5NeFxWvRyPIwyFRG3/gikzZ3O4QkD/3cZcFM/c2c+xYFMiubUtwikc8XFxxcNoRm+03rPeKpI2lcObv2LtzniaDZrIC2++wNhpbzC+ny+xq5eyZsupSqu2t49AkvJITwInHz+uBlnZBGsKf6eYCmLYtvxLIlJkDHhqKlOmvcCUF54nzC2Xbd//zJ8xWdimBqxT3TfdJUOWSNi4lMgkGT0nv8q4AaGoALfAnkx55UkamdKJjIynXuxKpsDZvRHBzf57TrsEkMkd8PULorG7/U2cLmKHs4MjDkUaysptY145JyLYty0K9/4zeG7KYBoCOPoz7JnpDOrsTOSW3dzYXXwnCIQoIS9NjpNfU9wtxf9VSJzdvIIjp0rpNvEVxg8MxQ5wC+rJ0y89jq+UQfiuaOrhzJMqVDu0NutLKcjO5GxaOsqmnegS7I1KcUOjjIWXOJ2QSFpeKUgmVJISj7YdaBvkj4d9bZpnJn79OkqaP0CHzvdRecOdRPLxI2SVehD6QChVtsoaS0g6EcuB40kYzRW2o8kUuPkE0r5zV9o287DIdLMIag6BuvmhdWHGMSLiSnjgoR74utjXeNc7x0Tc0tlMnJ/GYws/4O2xV04GqY6ynHMcic/E0S+E7qG+Vt5NkHX8MAnJRYQ8OgzL/WQl6mRiIzNp/lA/Aqv5/muYdQWcjj1Cgi6IsQNDrBwNZUaXvYMxvmMwfxTB9nd7W0lzZwhDGZlZqWSlZVFQokerLcauUQjt27ahqZcj19S69qG1mVO//0ahdys69OlAZbFEanw0aZftade3Y1W9tYZBQ/b5BBIy1Oh0WgwyOzyahtGlUwAut9jFWjFkiZLLF0hJTSYpPoLFP2zB/7mf+H5qD9yuBf+XZ7BjyfesiS/Fwd2Dxo5apORTxKkCefT52TzWIxiXGjRJiIoRaZWNpyYZAPknWPTRHGb/dAAfd0eEkCFXmNEUlOAeMJD3l3zPtN6WqmcrbtKQNRn89O9XeOt3A6vDVzEk0Jtajly6Y0pjljDi8ZU0f+nfzH914JUe1Bq6Av5eNZ+ZXx6h87Pvsfz1h6uuRVQqdit1cJ2aZCBMelIOb+KDt95nq+NMLv39KlWaWMlISdSXBD/4EU9sPcvXI6ru3LpTNLErmLfxGCqVK45KBwovxRCdbseQya8xfVR3Gl0ditVmyDXpZk0y65SRsm8Lv/60h6zAYAJkGrIvppNZ7Muo12by5IMtamyMLalq98JMXtYFLuaV4ta8AVwqx0khr3SSUUFSBN98vQNFr4l8/PlHzF/wOQu+eBaHfatZuyOa3LKaZ7eVh/mVP7gmGYAQdgR3G8G8r5azbs2v/PLrWtasWMhbz42jd88B9OlWV0Z8s2g5uXIRO2N1OLs5o6prC76KS2h7WvqVkZmSRk61i5uClJh9ROyJo1hywdXJzkoJWxa71RRXqUkmUZqbxK61O8ksd8LT3fqBD0LSk376DPm0pXenJpZim6DLTaJUHsSQ6bP5YO4cvvhpBX3dUjly8CAX828+AqUm3axJZo3yS/FsWLWOrbmteOHjObzz0Wd8Me8FutpF8OOSDaSUWOaomaqGLFPiF9qdAUPGMnTQAO5zsq+SqDg3G3WpK126BeJ5rTn370oHr0Y4mk3V+/tsgMyzJUPHPM1bU0fzYJ9+9O/Xm66+Ljga5TQbOIyWth6X3SJF51fz0eoEej7Sj6ZO8puoUhvh0o4hbb3QpieQfMm6FhjUEYQfikDv6kf7Vk1QSGar7h5bYNYXcCJyBfGaBvTtFIxcWHPOCMwmNdEHzqBoPpQuvnVTWl4D32fRvFfpHXB1Bm4WONk74e7ihKo+Tnyoghl1SiKx50x4PDKKa8fOKwPaMmBMf4ynjxGfVm1rbBUrXyHD3sEZRzsAI9fP8a5Aw+C2dGgrJ2ZXLMeTssjJzSXrQjTqhqH06RqCZ12uGsmV2KmUN17cnMEfO/cTn+PPo6ODrw5r7gYCY24yKz78mfLXvuPRTvbIr566Ws1Co41x4qHxnfG3zyY15RJVPKOGQnb9uJ54Q2MeeHQwgc5GzNLN9B23gaTjYnQE67Yk0uHFaYR4mpCs2TECY2EasecNhM16vM5CcuV2zjjZQan6MmmJ8fz149fEG7owaPAg7mtUe9CS7ZGhtHfA0d6Mtlhd4bqJMkmJXWk5xZqyCtdrx4oh145zi75MndSbE78vZ8XqDWzZuoGv3/2UxJCxPNS/HZ711isaubA/nP2p0HTy87S346aGNXWBZCwkdvsyjri+zpoJLZDJlFeis+ztMZfmotFbD3awJa69HifEWSIpNpYLxRWfpuX83pWEZ7akx7BZDA5xQmsChVKFAPTaMhseDmimKC2KPzbsxK7PDzzX3QuDCWRyBQpAV1aC4drMy6jj4tFo4j1aM39csMV9bIu5vIiEqD1sXLGQt97bjWdoX3p0CMKxDvuc6pHj6d+Kbu3c0R9ez4aoOM6cT+NETDzHDsaQ5+GOh/Ot+eFuy5AxFpJbpqVZ7y60DwvE38cb38BQ3BIPEHMsmaLbj/C8JUyFF4iIOEoBDRk/8C7OjSUzGcf+4OON0XTq5sTZqENExydTUpJL/JHDbFn+Hw6mGapGZNkaZUcG9G2JyDpDQtLF65cLzoazaGMkGnclAYoLHNoXz2V1HlnnjrP9jw2ERx2nwEZ1plOnsm3DSr47q2JQmIaoPQdJvFSAXp1ExL6dbNq5m2wtgECnuczfB2MJHTSVQdWuztkGuUKJS2M/wgaN5fm3e3Ah+gd+2riXzKJ63ysLgEOT+xk76RkmNi9m++KlrPh1N1FxeShR4uHlRhPvSmci1cptGfKlw5tYsOAUDz/9NNPGjWLoqAm8PH8eYQX7+GXJJhJz6/4YNYDMM8c5eamE5t36ElZvo4CqCMlExqlY8op0/Ll8Pv96+x0WLt1ORvpJli2Yy+KdiWht1+XVSMdhQ7nPTUfyiQTyjAB6Us9nUlJUzJmDG5n7+kzmfbueuNMnOLR1KV8v+Y2EbB3K2qLHbgZhpDQ3kxMJuajKk/j87Rd5e94iNkclUXx2G59+/BUHk4qQy68sql4+H0dUpj3jRna1vJNtERLYuxPapT8DHhrNtDcWMSYwi/17d5KUefWEwPpGZodvpyHMWrSMxV/PZ86/pvBY/wDsdbk4+7fAr5qtAtVRqyFfGaDJkF9fFDCSk55NYV4ZpYU6brRnLnj5yZGVaa7EvF6/XkdoL3Ms+hglwpN+/TpYSusVmdKe3tO+IibqMBER+9m/bz9/LJ1N+/sH88Pug4Tv/pOxbR3r/gA+wM6nGwN7tidPncTx8xcBezo/MoNfN/9F9KGDhP8dwb51CxjR/2Eef2cZEVt/440nB+KltEGNyVR4h/Zn0c9/Ehd1gL/+3s/ByG3MefxBGj34Dgf37mHx+9PwdwJDSSbRf+0hoPt0+rao4pSyKdrMWA4dO0te+bWYKyVe3s0wm8FgNNS9rtaEyh4XD3dcFRoS4/YTnujAoHFPE3RrI2vrhmzUl6HOyyYnJZGLZaVcTk8hLSMddbEegYpWnbrTqbuZPesOcOBICmmZ6Zw/vIqD6Xa07v8gQV7X/t9r3ZF1ci+xx07SoP1wOgXc4lffEVerXSZHWY2jT0ilpJzPoCQrg+NxSZRa/n+fOkVOx6H9aedVSHR4JGcyLSO9TGRmZpGfkUn62STSrw8U6qLGzBRmppN5MY+ylASOlV4xGkmXz7lDG9ib1ZBxk/vYbDtkdRQf/Ia35/ybX/6OJDHjIolx+zl2Adq160izxh7Xv1ymVCCvn5XJ6xj1peQkJxC5dRsbdyfjMvIdnn7o1ucZirlz586tfEmgzjzOji3LWLN2P+cLdZQXZpF3MZkccwtCgz1xbhLIfQGuZEbFsj/ybw4f+otjkWmEPDGLZx5/mGBPVZ2oxQ10JETuJua0oNdTk+lQ64Zd22E2qjm07DuO6FvyQPc2yDUaFG4eOFQYmhrK4lj9nzUkqvNJT3Om6+iu+Cjr0RWl8uD+EF9yos5TrHUgIKTR9eACXWEKEdt2cujISfKKFTTwbUmb+7yqBoXYAJO+iDP7d/D7thhKDWUYCKRr90BkOSfYvvcS/WbMolujup8TOTr4YihO5HD0AQ6FH+DvM6dxajmIiRNG0C7QE6HJ5WJOPlmJR1i/eRf27UYzuEcoXjcTnXVHSOSkRrF++VJOiib0eOQppo/vRUPlzQSUVMZKZBcIIWE2mTALGUqlAiQzkhDI5EqUlfxuEiajCbMkkCvsUNUeFGwjrvwzLoGsziOmKiMwalNZNqEfC07ZoZTLUChDmRu+lccrrrUJCZNJQq6QYTYJlHbKW6wWGyHEla2T8gqNiBCYr/mdhACZHEWd+VIFklm69hgkMyhUCmRCINV73YFkMmKSpCsuzAqLApl/zGPmgg3EZWiRtMUMf38ds6cMJLAePFNCkjCbzchVKuvD45vEqiHf4x7/b6gcW1lRcMu94t3kThqBe9zjfx+rRsz/lBFzz5DvcY9/Bv8Ha9yIh1L6q0UAAAAASUVORK5CYII=" alt="" />Solution
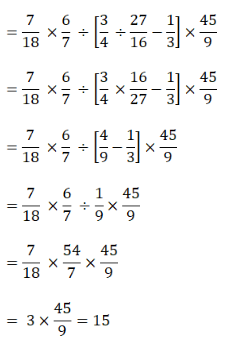
If perpendicular and base of a right-angle triangle is, 14 cm and 48 cm, respectively, then find the length of the shortest median of triangle.
Calculate the hypotenuse of an isosceles right-angled triangle where the equal sides are 8√6 cm each.
- The sides of two similar triangles are in the ratio 5:7. The areas of these triangles are in the ratio:
Area of a triangles with vertices at (2, 3), (-1, 0) and (2, -4) is :
What is the area of triangle ABC with vertices A(1, 2), B(5, 6), and C(7, 2)?
- The sides of a triangle are in the ratio 7:24:25. If the area of the triangle is 336 cm², what is the perimeter of the triangle?
In the given figure, AB ∥ QP, AB = x, PQ = x + 10, RB = x/2, BP = x + 1. Find PQ.
A triangle has sides 13, 14, 15. Find its area.
If the inradius of a triangle with a perimeter of 60cm is 8 cm, then find the area of the triangle.(in cm2)
- Find the area of a triangle with a base of 12.6 cm and a corresponding height of 18.4 cm.
Relevant for Exams:



