Question

    The Jar contains only 8 litres of milk and the rest is

    water. A new mixture in which concentration of milk is 30%, is to be formed by replacing the Jar mixture. How many litres of mixture shall be replaced with pure milk if there was initially 32 litres of water in the mixture?
    A 10 litres Correct Answer Incorrect Answer
    B 3 litres Correct Answer Incorrect Answer
    C 12 litres Correct Answer Incorrect Answer
    D 5 litres Correct Answer Incorrect Answer

    Solution

    Milk : water 8 : 32 Ratio = 1: 4 Initial mixture = 8 + 32 = 40 litres Using Allegation method, 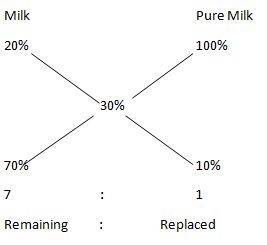Initial Mixture = 8 unit → 40 litres 1 unit = 5 litre The mixture of water and milk is replaced by 5 litres. Alternate method: As we know that mixture replaced in the same ratio in which original mixture was there. Let milk & water replaced out of mixture is x & 4x respectively. So, milk/water = (8-x+5x)/(32-4x) = (30%)/(70%) = 3/7 or 56+28x = 96-12x or 40x = 40 or x = 1 Hence, quantity of milk & water replaced is 1 & 4 L respectively. Therefore the mixture of water and milk is replaced by 5 litres.

    Practice Next
    More Mixture Questions

    Relevant for Exams:

    ask-question