Question
The length of a rectangle is 7 metres more than its
width. If the perimeter of the rectangle is 74 metres then what is the area (in m2 ) of the rectangle?Solution
Let the width of the rectangle = ‘x’ metres Then, length of the rectangle = (x + 7) metres Perimeter of the rectangle = 2 × (length + width) Or, 2 × (x + x + 7) = 74 Or, 2x + 2x + 14 = 74 Or, 4x = 74 – 14 = 60 Or, x = 60/4 = 15 m So, area of the rectangle = x × (x + 7) = 15 × 22 = 330 m2
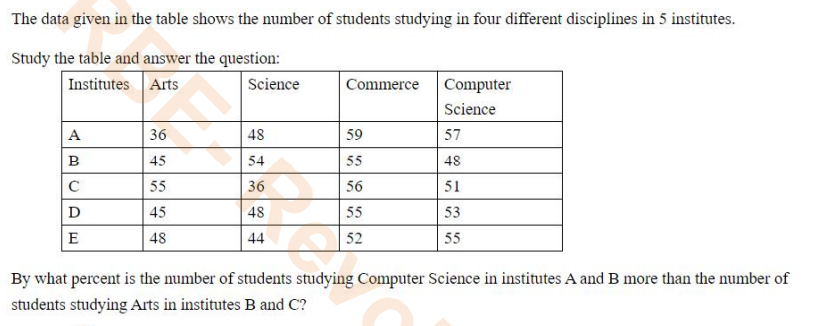
- Sneha spent 18% of her income on donations and out of the remaining amount, she spent 22% on household expenses, 28% on shopping, 12% on transportation, an...
- Riya spent 40% of her income on groceries and 50% of the remaining on entertainment. If she saves Rs. 1800 after these expenses, what is the amount spent o...
What is the rate of interest (in %) if simple interest earned on a certain sum for the 3rd year is Rs 2,000 and compound interest earned in 2 years is ...
A, B, C, and D purchased a cine-multiplex for Rs. 56 lakhs. The contribution of B, C, and D together is 366.66% that of B’s contribution and contribut...
In a colony, there are 60 APL families and 30 BPL families. Each APL and BPL family got blankets equal to 22% and 70%, respectively of total number of f...
- The strength of a club was 800 members in 2014. It rose by 40% in 2015, fell by 25% in 2016, and rose again by 15% in 2017. What was the total strength at ...
Suyash have total amount of Rs.2000 out of which, he spent 20% on food, 35% of the rest on travelling. Out of remaining amount he spends Rs.550 on misce...
A spent 20% and 30% of his monthly salary on food and rent, respectively. Of the remaining amount, he gave 15% and 20% to his mother and brother, respec...
In a school with 2,400 students, 45% of the students prefer indoor games, while the remaining students prefer outdoor games. Among those who prefer indo...
Relevant for Exams:



