New FLASH SALE Dhamaka - Flat 60% Off on All Courses

    Question

    Two ships are on opposite sides in front of a lighthouse

    in such a way that all three of them are in line. The angles of depression of two ships from the top of a lighthouse are 30° and 60°. If the distance between the ships is 230√3  m, then find the height (in m) of the lighthouse.
    A 145.2 Correct Answer Incorrect Answer
    B 172.5 Correct Answer Incorrect Answer
    C 160.5 Correct Answer Incorrect Answer
    D 135.4 Correct Answer Incorrect Answer

    Solution

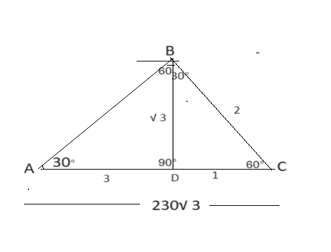    Let the length of the lighthouse = BD m Use this property - When the angles of a triangle are 30 ° ,60 ° , and 90° respectively, the ratio of the opposite sides is 1: √ 3:2. When Triangle BDC – The opposite side of angle 30° = 1 Similarly - angle 60° =       √ 3, and angle 90° =2 Triangle ABD -opposite side of angle 30 ° =BD = 1= √ 3……. means √ 3times. so -opposite side of angle60° =AD = √ 3 = √ 3× √ 3 =3 now – AD + DC = AC 4= 230 √ 3 1= (230 √ 3)/4 Now height = BD = √ 3= (230 √ 3/4) × √ 3= (230 ×3)/4 =690/4 =172.5meter

    Practice Next

    Relevant for Exams: