Question
Two chords, AB and CD, of a circle intersect at an external
point E. Given that the lengths of BE and DE are 12 cm and 8 cm, respectively, and the total length of chord AB is 36 cm, determine the length of chord CD.Solution
BE = 12 cm, DE = 8 cm, and AB = 36 cm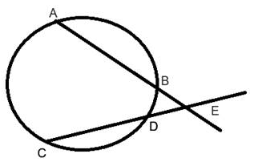
From the secant theorem:
AE X BE = CE X DE .... (I)
AE = AB + BE = 36 + 12 = 48 cm
Put the value of AE in equation (I) , we get,
48 X 12 = CE X 8
Or, CE = 48 X 12 X (1/8)
So, CE = 72 cm
Therefore, the length of the chord CD = CE - DE = 72 - 8 = 64 cm
Four of the following five figures are alike in a certain way and thus form a group. Which is the one that does NOT belong to that group?
Three different positions of the same dice are down. Select the number on the face opposite to the face showing ‘1’.
In a certain code language, 'PLIERS' is coded as MMAFJO and 'SHOVEL' is coded as FZRLFR. How will 'WRENCH' be coded in the same language?
By interchanging which two signs and two numbers (not digits) the equation will be correct?
8 – 4 × 9 + 6 ÷ 3 = 29
If 'I' stands for '+', 'J' stands for '×', 'K' stands for '÷' and 'L' stands for '–' what will come in place of the question mark (?) in the followi...
Which of the following numbers will replace the question mark (?) in the given series?
15, 27, 12, ?, 9, 33
Select the correct mirror image of the given figure when the mirror is placed at MN as shown below.
Â
Statement: H
F ≥ U = M conclusion:
i) M> I
ii) P>
iii) H
In a certain code language, 'FIRE' is coded as '7391' and 'AGED' is coded as '8247'. What is the code for 'E' in the given code language?
Select the option that is related to the third word in the same way as the second word is related to the first word (The words must be considered as mea...
Relevant for Exams:
