Question
A circle with centre 'O' has a radius of 39 cm. If the
length of cord PQ is 72 cm, then find OA:OP, given that PA:PQ = 1:2 and the points 'P', 'A' and 'Q' are collinearSolution
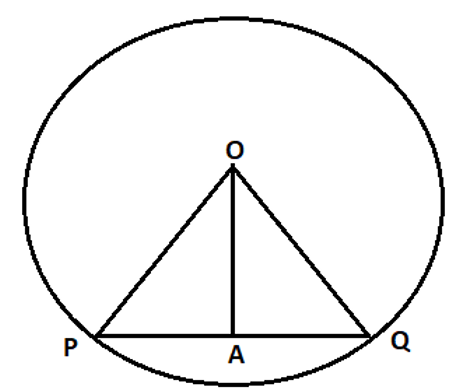In right triangle AOP, OP = 39 cm Also, (PA/PQ) = (1/2) Or, (PA/72) = (1/2) So, PA = 36 cm We know that the perpendicular drawn through the circle bisects the chord. So, ∠PAO = ∠PAQ = 90o So, OA2 = OP2 - PA2 {Using Pythagoras theorem} Or, OA = √(1521 - 1296) = 15 cm So, required ratio = 15:39 = 5:13
Which of the following projects is part of the ₹57,000 crore investment at Kandla Port?
The Adani Group has sold around 3% stake in Adani Transmission through open market transactions to raise about______.
How much annual transit fee will Afghanistan receive from the TAPI pipeline project?
Who embarked at sea to witness the Indian Navy’s ability to conduct 'twin-carrier operations' during the inaugural session of the first edition of the...
The government has mandated all private companies, other than small companies, to dematerialise their shares by _________ & is expected to boost transpa...
What is the primary purpose of the geospatial foundation model unveiled by IBM and NASA?
In which corridor of the Kaziranga-Karbi Anglong Landscape was the dhole recently photo-captured?
According to a UN report, what is causing the world’s water cycle to become increasingly unpredictable?
Which rocket was successfully launched by Europe after a four- year delay?
What is the total amount the Asian Development Bank (ADB) plans to mobilize over five years to support India’s urban infrastructure development?
Relevant for Exams:
