Question
A cube has six faces, each of a different colour. The
red face is opposite to black. The green face is between red and black. The blue face is adjacent to the white. The brown face is adjacent to the blue. The red face is the bottommost face. The face opposite to the brown face isSolution
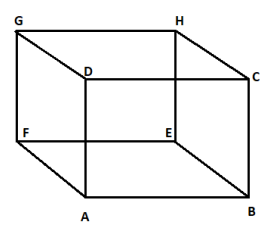ABEF = Red GHDC= Black ABCD = Green EFGH = Blue AFGD White BCHE Brown So, White is opposite to brown face.
How many floors are there in between the floor of the one who likes Yellow and the one who lives at floor 8th?
Who lives to the immediate east of Swati?
Four of the following five are a like in a certain way based on the given arrangement and thus form a group. Which is the one that does not belong to ...
Six boxes L, M, N, O, P and Q are kept one above another. The bottommost box is numbered as 1 and the topmost box is numbered as 6. L is three boxes bel...
Which of the following statement is/are not true?
I. One person was born between C and the one who likes Mysore.
II. The one who likes Har...
Who likes Sanskriti school?
A series is given with one term missing. Choose the correct alternatives from the given ones that will complete the series.
17, 21, 46, 52, 101, ...
What is the difference between the floor number of O and N?
Which of the following combinations of day-person-company-colour is correct?
What is the position of R with respect to T?
Relevant for Exams:
