Question
There are three envelopes with three different
addresses writen on them. Three leters are to be enclosed in these three envelopes such that one leter goes inside one envelope without seeing the address writen on any envelope. What is the probability that each of the three leters goes into the envelope with correct address writen on it?Solution
Total no. of ways =3!=6 and favourable no.of ways =1. So, required probability = 1/6
क्ष, त्र और ज्ञ की गणना स्वतन्त्र वर्णों में नहीं होती क्य�...
निम्न में से कौन सार्वनामिक विशेषण का उदाहरण है?
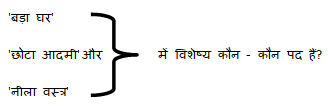
'गुरुकुल' शब्द में कौन सा समास है?
'र' का विवरण है
मुख्य क्रिया के अर्थ को स्पष्ट करने वाली क्रिया होती है
अन्नजल में कौन सा समास है
जंहा मुफ्त में खाना बंटता हो ,उसके लिए एक शब्द क्या होगा ?
दिए गए शब्दों के शुद्ध वर्तनी के लिए चार विकल्प दिए गए हैं�...
निम्नलिखित में से कौन – सा सुमेलित युग्म नहीं है?
Relevant for Exams:



