Question
Who lives three floors above
V? Study the following information and answer the given questions. In an eleven-story building, having floors numbered 1 to 11, Z, Y, X, W, V, U, T, S, and R each live on a different floor. The ground floor is numbered floor number 1, the floor above it is numbered 2 and so on. Two of the floors in the building are vacant. Z lives on the fifth floor. None of the vacant floor is an odd-numbered floor. There are three floors between the floors on which Y and W live. V does not live on a floor immediately above or immediately below X’s floor. There is one vacant floor between the floors on which S and T live. The number of floors between the two vacant floors is the same as the floor number on which W lives. V does not live on an odd – numbered floor and U lives below Z. Only W lives between V and U. S lives on a prime numbered floor. X lives on an odd-numbered floor. X lives below T’s floor. R lives on an even numbered floor.Solution
(i) Z lives on the fifth floor. (ii) V does not live on an odd – numbered floor and U lives below Z. Only W lives between V and U. (iii) There are three floors between the floors on which Y and W live. (iv) S lives on a prime numbered floor. There will be two cases: It is given that Z lives on the fifth floor. If V lives at floor no. 2, then W and U live at 3 and 4 respectively. Y lives at floor no. 7. If V lives at floor no. 4, then W and U live at 3 and 2 respectively. Y lives at floor no. 7. S lives at floor no. 11. 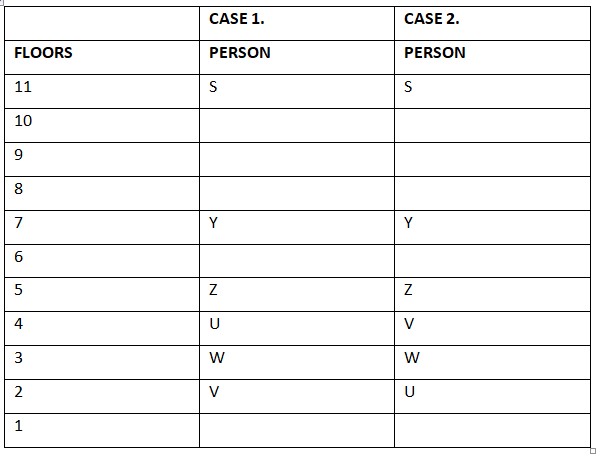 (v) None of the vacant floor is an odd-numbered floor. (vi) V does not live on a floor immediately above or immediately below X’s floor. There is one vacant floor between the floors on which S and T live. (vii) The number of floors between the two vacant floors is the same as the floor number on which W lives. (viii) X lives on an odd-numbered floor. X lives below T’s floor. R lives on an even numbered floor. T lives at floor no. 9 and vacant floor is floor no.10. We know that W lives at floor no. 3. So, there will be gap of three floors between vacant floors. Other vacant floor is floor no. 6. Case 1 will get discarded as X will live at floor no. 8 but X lives on an odd-numbered floor.
(v) None of the vacant floor is an odd-numbered floor. (vi) V does not live on a floor immediately above or immediately below X’s floor. There is one vacant floor between the floors on which S and T live. (vii) The number of floors between the two vacant floors is the same as the floor number on which W lives. (viii) X lives on an odd-numbered floor. X lives below T’s floor. R lives on an even numbered floor. T lives at floor no. 9 and vacant floor is floor no.10. We know that W lives at floor no. 3. So, there will be gap of three floors between vacant floors. Other vacant floor is floor no. 6. Case 1 will get discarded as X will live at floor no. 8 but X lives on an odd-numbered floor. 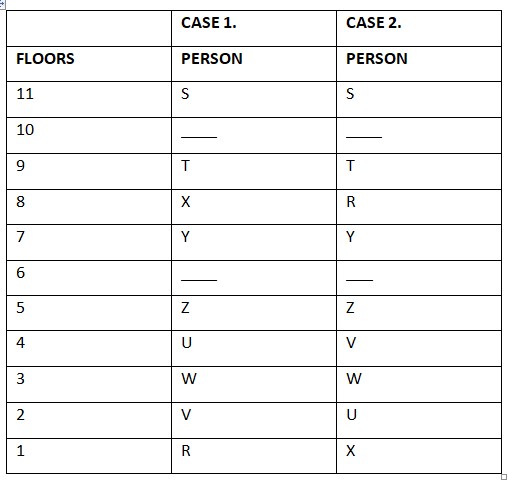 Final arrangement as shown below:
Final arrangement as shown below: 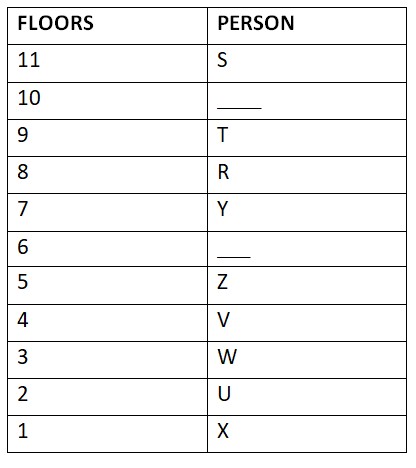
As a performance measure, share of voice is
Which of the following statements demonstrates the formation of a segment based on family size?
Within the buying centre, influencers are people who:
Which method of classifying retail outlets would be most appropriate for describing McDonald's, Holiday Inn, and Subway-all franchise operations?
The Marketing Manager at Pepsi describes to a new employee that her first major task is to develop a road map for Pepsi One. The new employee is confuse...
The type of need which puts a boundary to specified needs is known as ___________.
Intermediaries make the selling of goods more efficient by:
A web page that serves as a publicly accessible personal journal and online forum for an individual or organization is referred to as a:
As a step towards reducing our carbon footprint, the government recently made subsidies available to citizens who made their homes more energy-efficient...
A single social media site like Facebook or YouTube is referred to as a
Relevant for Exams:


