Question
‘A’ and ‘B’, alone can complete a work in 25
days and 50 days, respectively. Both of them started the work together but ‘A’ left the work when 2% of the work was remaining which is then completed by ‘B’ alone, then find the total time required to complete the whole work in this way.Solution
Let the total work be 250 units {L.C.M of 25 and 50 units} Efficiency of ‘A’ = (250/25) = 10 units/day Efficiency of ‘B’ = (250/50) = 5 units/day Remaining work = 0.02 × 250 = 5 units Number of days taken by ‘A’ and ‘B’ to complete 245 units = 245/(10 + 5) = 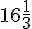 days Number of days taken by ‘B’ to complete 5 units of the work = (5/5) = 1 day Total time taken to complete the work =
days Number of days taken by ‘B’ to complete 5 units of the work = (5/5) = 1 day Total time taken to complete the work = 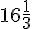 + 1 =
+ 1 = 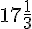 day
day
The average monthly expense of a family of 5 is ₹25,000. If the highest earning member moves out, the average drops to ₹20,000. Find the monthly exp...
A number is such that when it is multiplied by 9, it gives another number which is as much above from 420 as the original number (itself) is below 420. ...
Average of 15 observations calculated by a student was 70 but when he again went through his observations he realised that he took value of three observ...
- The average salary of A, B, and C is Rs. 30000 and the average salary of D and E is Rs. 25000. If the savings of A is 40% of the average salary of all five...
Ravi scored 95, 88, 102, 110, 76 and 91 marks in History, Chemistry, Biology, Mathematics, English and Computer respectively. What is the average of his...
In 40 matches, Mia had a bowling average of 18.6. She played 3 more matches, took 3 wickets after conceding 162 runs, and her average increased by 1.8. ...
Average of 20 numbers is 90. Average of first 8 numbers is 103 while average of last nine numbers is 40. If ninth number is 25% less than the tenth numb...
If the average of 38, 49, 42, and 'b' is 50, then find the value of '2b'.
In a workshop with 20 participants, the average productivity score is 90. One person with a score of 85 leaves, and 3 new participants with an average s...
Each question contains a statement followed by Quantity I and II. Read the information clearly and answer your questions accordingly.
Qu...
Relevant for Exams:


