Question
While going to a destination after travelling 75km, the
driver noticed some problem in the clutch of the bus due to which he had to proceed at 2/5 of its former rate and reached the destination 5 hours late. Had the problem in the clutch happened 15 km further on, it would have arrived 30 minutes sooner. Find the speed of the bus and total distance covered by the bus?Solution
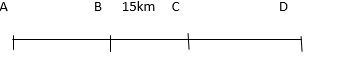Let A is the starting point and B is actual point where bus met with an accident C is the assumed point bus met with an accident Given BC = 15km and Difference of is 30 minutes basically due to the speed covering this 15km. Let original speed = x km/hr Speed after clutch problem = (2x)/5 km/hr ⇒ 15/((2x)/5)-15/x=30/60 ⇒ 75/(2x)-15/x=1/2 ⇒ (75-30)/(2x)=1/2 ⇒ 45/(2x)=1/2 ⇒ x = (45 × 2)/2 x = 45 km/hr Let the distance be ‘D’ km Time taken at original speed =D/45 hr……….(i) Time taken after clutch problem took place at 75 km distance = (75/45)+(D-75)/(45×(2/5)` = 75/45+(5(D-75))/(45×2) = 5/3+((D-75))/18 = (30+D-75)/18 = (D-45)/18 ………………………..(ii) As per the question, (ii) – (i) = 5 hours (D-45)/18-D/45=5 = (5D-225-2D)/90=5 = (3D-225)/90=5 3D – 225 = 450 3D = 675 D = 225 km
According to section 32 of the Specific Relief Act an instrument can be cancelled in part when
Void Agreement signifies_____________
Under the definition of “approved securities” in Section 5(a) of the Banking Regulation Act, 1949, as substituted by the Banking Laws (Amendment) Ac...
Indian Evidence Act was drafted by:
The Constitution of India is
According to the IRDA Act, 1999 intermediary or insurance intermediary includes_________
What are Eligible Companies under section 76 of the Companies Act, 2013?
Who among the following is a 'holder in due course' under Section 9 of the Act?
Under Section 11, what is the maximum age up to which the Chairperson of the DRAT can continue to serve?
Under Section 30B of the SARFAESI Act, an appeal against the order of the adjudicating authority imposing penalty under Section 30A must be preferred wi...
