Question
A two-digit number decreases by 54 when its digits are
reversed. If the sum of its digits is 10, what is the original number?Solution
For the original number, let the unit digit and ten’s digit be ‘y’ and ‘x’, respectively.
So, the original number = (10x + y)
Now, if the digits are reversed, the new number = (10y + x).
ATQ, (10x + y) – (10y + x) = 54
Or, 9x – 9y = 54
So, x – y = 6……….(i)
And, given that, x + y = 10………(ii)
By adding equation (i) and equation (ii), we get,
2x = 16
So, ‘x’ = 8
And, ‘y’ = 2
So, the original number = 10x + y = 10 × 8 + 2 = 80 + 2 = 82
How is G related to H?
Read the given arrangement of numbers, letters, and symbols carefully and answer the questions based in it.
% 7 @ 8 3 % 9 N 4 7 M @ 6 N & 9 R #...
Read the directions below and answer the following questions.
Six persons Monu, Gita, Dev, Sonu, Golu, and Uma live in a six-floored building. ...
I n the question, assuming the given statements to be true, find which of the conclusion (s) among given three conclusions is /are definitely true and t...
Read the given statements and conclusions carefully. Assuming that the information given in the statements is true, even if it appears to be at varianc...
- Find the missing number in the diagram given below.
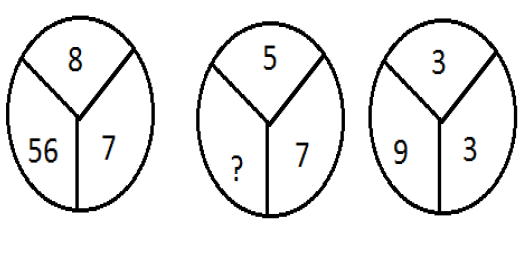 <...
<... If a meaningful four-letter English word is formed by using the 2nd, 5th, 6th and 10th letter (from the left end) of the word ‘COMPONENTS’ then whic...
In this question, the relation between various elements is shown in the statement. After the statement, two conclusions are given, select a suitable op...
In a certain code language, ‘COLD’ is written as ‘FLOA’, and ‘WARM’ is written as ‘ZXUJ’. How will ‘HEAT’ be written in that languag...
In the question below some statements are given followed by three conclusions I, II and III. You have to take the given statements to be true even if t...
Relevant for Exams:


