Question
‘x’ litres of mixture ‘A’ contains milk and
water, only in the ratio of 6:5, respectively. 90 litres of mixture ‘B’ contains 25% more water than milk in it. If both the given mixtures are mixed together, then ratio of quantity of milk to that of water in the resultant mixture becomes 10:11, respectively. Find the value of ‘x’.Solution
Mixture A (x litres): Milk = (6/11)x Water = (5/11)x Mixture B (90 litres): Milk = 40 Water = 50 Equation: ( (6/11)x + 40 ) / ( (5/11)x + 50 ) = 10 / 11 Cross multiply: 11((6/11)x + 40) = 10((5/11)x + 50) 6x + 440 = (50/11)x + 500 6x – (50/11)x = 60 (16/11)x = 60 x = (60 × 11) / 16 x = 41.25
What will come in the place of question mark?
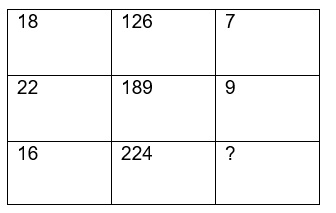
What number should replace the question mark?
C/JQ : B/GT : : Z/CX : ?
M/14 : O/12 : : U/6 : ?
Study the given pattern carefully and select the number that can replace the question mark (?) in it.
First row: 14, 12, 108
Second row:...
Find the missing term in the following series:
43 44 ? 69 185
...Find the missing number.
F : 216 : : I : ?
In each of the following questions select the related letter/word/figure/number from the given alternatives.
JRH : ? : : KOV : 51
Find the next term / numbers in the given series?
54, 46, 40, 36, ?
Relevant for Exams:


