Question
AB is the diameter of a circle with center o. P is the
point on it If the cone ∠AOP is equal to 98 degrees then ∠OBP will be.Solution
∠ AOP = 98° ∠ POB = (180° - 98° ) = 82° Δ POB = ∠ P = ∠ B (Isosceles triangle) ∠ POB = 82° Δ ΡΟΒ = ∠ POB + ∠ OBP + 2 BPO = 180° 180° = 82°+ 2 x ∠ OBP 98/2 = ∠ OBP 49° =∠ OBP ∠ OBP =49° 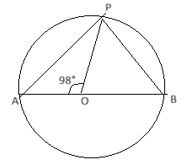
With reference to the office of the Attorney General of India, Which of the following statements is/are correct?
I. He is the highest law offic...
Saikhom Mirabai Chanu is an _______ .
Which of the following referred to as ‘paper taxes’?
I. Weather tax
II. Gift tax
How many planets are terrestrial planets?
Who heads the Inter-Ministerial Committee on Investment in Critical and Foreign Technologies (IMICF)?
Which symbiotic bacterium is responsible for nitrogen fixation?
What is the maximum application amount that individuals can utilize UPI for, as per the guidelines issued by SEBI for public issues of equity shares and...
Who was the first woman to receive the Arjuna award for Hockey?
Consider the following statement about the peace agreement done by Government of India in December 2023:
1. It was signed between United Nation...
RBI has launched the Payments Vision document 2025 with the theme of:
Relevant for Exams:



