Find the area of maximum side of square that can be inscribed in a right angled triangle of side 15, 20 and 25 cm.
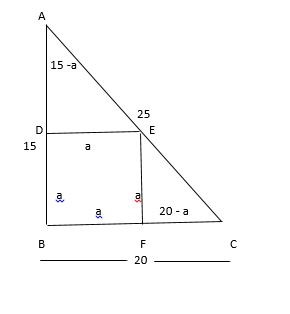Let the side of the square be a Then, AD = 15 – a and FC = 20 - a Area of Triangle ABC = 1/2 × Base × Height = 1/2 × 15 ×20 = 150 cm² Now, Area of Triangles ADE and EFC + Area of Square BDEF = Area of Triangle ABC ∴ 1/2 ×a × (15 - a) + 1/2 × a × (20 - a) + a² = 150 15a/2 - a²/2 + 10a - a²/2 + a² = 150 (15a+20a)/2 = 150 35a = 300 a = 300/35 = 60/7 cm Area of Square = 3600/49 cm²
The company's CEO decided to ____________ the new marketing campaign due to budget constraints, even though it showed promising results in initial test...
Insurance law has to be revisited to ensure that there is guarenteed renewal of policies.
This statement is________.
Choose the word which is the most opposite in meaning to the word ‘vested’ as used in the passage.
Private sector lendors have been found guilty of _________________ ?
Which of the following is definitely not true according to the passage?
Antonym of revitalize
Choose the word which is the most opposite in meaning to the word ‘insinuating’ as used in the passage .
CONSENSUS
Which one of the following maybe a suitable meaning of the following phrase ‘raised dust and storm’ as used in the passage above.
...Choose the word which is the most opposite in meaning to the word ‘insinuating’ as used in the passage .
