Question
In a given figure, ABCD is a parallelogram, P and Q are
the mid points of sides CD and BC respectively. Then the ratio of area of shaded portion: area of unshaded portion isSolution
Let the total area of parallelogram = 32 units Area of parallelogram AXPD = 32/2 = 16 units Area of ∆APD = 16/2 = 8 units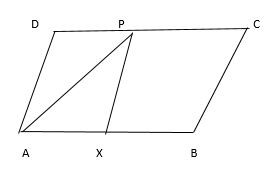 
Area of parallelogram ABQY = 32/2 = 16 units Area of ∆ABQ = 16/2 = 8 units 
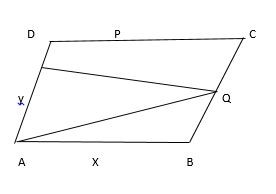Area of parallelogram AOCQ = 32/4 = 8 units Area of ∆PQC = 8/2 = 4 units 
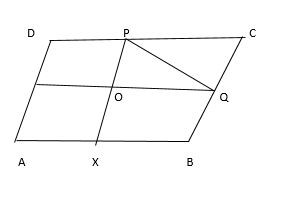Area of ∆PQA = 32 - 20 = 12 units 
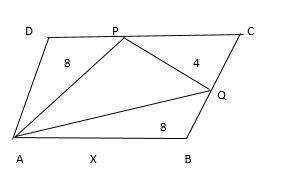∴ Area of shaded portion : Area of unshaded portion = 20 : 12 ⇒ 5 : 3
In which of the following years was the ‘Project Elephant’ launched by the Government of India?
Name the award received by the following scientists in January 2023.
1. Shri Khadar Valli Dudekula
2. Shri Modadugu Vijay Gupta
3. ...
NBFCs were the largest net borrowers of funds from the financial system, which of the following was second highest net borrowers of funds from the finan...
Salt Satyagraha was associated with the:
The Reserve Bank of India has allowed banks to use ratings from Brickwork Ratings India Private Limited for loans up to Rs. _________.
The Right to Freedom of Religion is covered under which Articles of the Constitution of India?
The Veda Samaj was established in ______.
Whose autobiography is titled 'An Unsuitable Boy'?
Which of the following options are all transition metals?
History of Akbar’s region, titled “Akbar Nama” is written by ____.
Relevant for Exams:
