Question
In an acute-angled triangle XYZ, an altitude XP is drawn
from vertex X to side YZ. A point O is located on XP such that XY = 12 cm, OY = 5 cm, and OZ = 9 cm. Determine the length of XZ.Solution
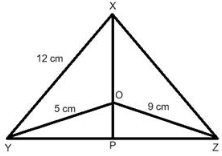Since, XP ⊥ YZ, both ΔXYP and ΔOYP are right triangles.Similarly, both ΔXZP and ΔOZP are also right triangles.Using Pythagoras theorem, we have;In ΔXYP, XY2 = YP2 + XP2Or, XP2 = XY2 - YP2 ....... (I)And ΔXZP, we have;XZ2 = XP2 + PZ2So, XP2 = XZ2 - PZ2 ...... (II)So, XY2 - YP2 = XZ2 - PZ2Now, using equation (I) and (II) , we have;Or, XZ2 - XY2 = PZ2 - YP2 ...... (III)Now, in ΔOYP, we have;And OP2 = OY2 - YP2 ....... (IV)And in ΔOZP, we have;OP2 = OZ2 - PZ2 ...... (V)Now, using equation (IV) and (V) , we have;OY2 - YP2 = OZ2 - PZ2Or, PZ2 - PY2 = OZ2 - OY2 ...... (VI)Now, using equation (III) and (VI) , we have;OZ2 - OY2 = XZ2 - XY2Or, XY2 + OZ2 = XZ2 + OY2So, 122 + 92 = XZ2 + 52Or, 144 + 81 = XZ2 + 25Or, XZ2 = 225 - 25Or, XZ2 = 200And XZ = ± 10√2Since, side of a triangle cannot be negative, XZ = 10√2 cm
In the given number ‘453976394’ if ‘2’ is subtracted from each odd number and ‘2’ is added to each even number then how many digits are rep...
If all the digits of the number 854237352878 will be arranged in descending order from the right end, then, what will be the sum of 3rd, 5th, 9th, and ...
All the letters of the word ‘INTERCEPT’ are arranged in alphabetical order from left to right. Then all the consonants are replaced with the...
When the vowels of the word HIMALAYA are replaced by their immediate successive letter and the consonants are replaced by their immediately preceding le...
How many such pair(s) of letters are in the word “ENQUIRY” which has as many letters between them (both forward and backward) as in the English alph...
When letters of the word ‘MONETISATION’ are arranged in reverse alphabetical order from left to right, then how many vowels are there between S and ...
How many pairs of letters are there in the word 'REQUIREMENT' which has as many letters between them (both forward and backward) in the word as in the E...
When all the digits of the number ‘385967368578’ are arranged in increasing order from the left end, then what is the number obtained when third dig...
- If we arrange all the letters of the word ‘’ASSIGNMENTS’ in alphabetical order from the left end, then, which letter will remain at its initial posit...
How many pairs of letters are there in the word ‘PARACETAMOL’ which has as many letters between them in the words as in the English alphabetical ser...
