New FLASH SALE Dhamaka - Flat 60% Off on All Courses

    Question

    ABC is an isosceles triangle inscribed in a circle. If

    AB = AC = 12√5 and BC = 24 cm then radius of circle is
    A 10 cm Correct Answer Incorrect Answer
    B 15 cm Correct Answer Incorrect Answer
    C 12 cm Correct Answer Incorrect Answer
    D 14 cm Correct Answer Incorrect Answer

    Solution

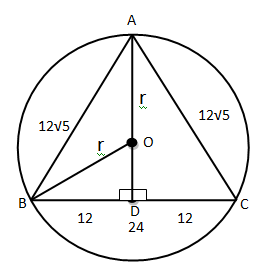    we know if we draw a Ʇ which AD is bisect BC in two equal part BD = DC = 12 Now apply PGT in ∆ADC AD = 24 If 0 in centre of circle. then OD = (24 – r) Now apply PGT in ∆OBD we get r2 = (12)² + (24 – r)2 r2 – (24 – r )2 = 12² (r + 24 – r )(r – 24 + r) = 144 2r = 24 + 6 = 2r = 30 = r = 15

    Practice Next

    Relevant for Exams: