Question
AB and AC are two tangents of a circle of centre O with
radius 5cm. Another tangent is drawn on the circle which intersects AB and AC at m and n respectively. Find the shortest length of mn, if the length of tangent AB is 12cm?Solution
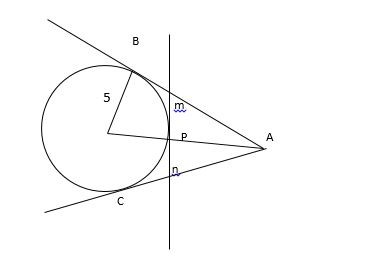AO² = AB² + OB² AO² = 5² + 12² = 169 AO = 13cm Let P be the point which divides MN in two equal parts Now, In Triangle BOA and MPA ∠BAO = ∠MAP and ∠OBA = ∠MPA Therefore both the Triangles are similar, Hence AP/AB = MP/OB 8/12 = MP/5 MP = 10/3 Length of the Shortest Tangent = 2 ×10/3 = 20/3 cm
Justice Revati Mohite Dere was sworn in as the first woman Chief Justice of which High Court?Â
Who won the Belgian Grand Prix after George Russell's disqualification?
- Which Indian state became the top recipient of Foreign Direct Investment (FDI) in FY25?
In which river will India’s first solar-powered boat be launched?
Which entity recently launched the second international banking centre in Chennai to cater to the financial needs of global Indians?
Who won the Prime Minister election in Mauritius on November 11, 2024?
Which state recently joined the Ayushman Bharat PM-JAY scheme?
- Which central agency approved the River Cities Alliance (RCA) master plan?
Government has advanced the target of 20% ethanol blending in petrol from earlier 2030 to ______.
REC Limited has signed an agreement with which organization to aid in the education of approximately 75,500 children in the Siddharthnagar, UP?
Relevant for Exams:
