📢 Too many exams? Don’t know which one suits you best? Book Your Free Expert 👉 call Now!
  • google app store apple app store
    • ✖

      Question

      A football team of 11 players is to be formed from 20

      players including 5 defenders and 4 goal keepers. In how many different ways can a team be formed so that the team contains exactly 2 goal keepers and at least 3 defenders?
      A 44630 Correct Answer Incorrect Answer
      B 43560 Correct Answer Incorrect Answer
      C 48640 Correct Answer Incorrect Answer
      D 42660 Correct Answer Incorrect Answer
      E None of these Correct Answer Incorrect Answer

      Solution

      Total number of Defenders = 5 Total number of Goal keepers = 4 Total number of Normal players = 11 [20- (5+4)] Possible Combinations : ∴ Required Number of ways = (5C3 × 4C2 × 11C6) + (5C4 × 4C2 × 11C5) + (5C5 × 4C2 × 11C4) = 5!/(3! ×2!) × 4!/(2! ×2!) × 11!/(6! ×5!) + 5!/4! × 4!/(2! ×2!) × 11!/(5! ×6!) + 5!/5! × 4!/(2! ×2!) × 11!/(4! ×7!) = 10 × 6 × 462 + 5 × 6 × 462 + 1 × 6 × 330 = 27720 + 13860 + 1980 = 43560

      Practice Next
      More Data Interpretation Mains Questions

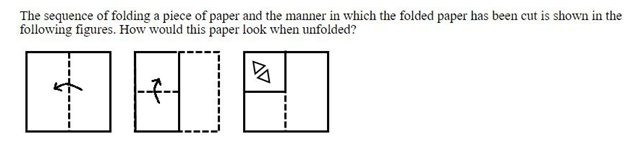
      Relevant for Exams:

      ask-question