Question

    Seven people Ian, Jen, Kia, Lex, Mia, Nia and Oji, are

    sitting in a straight row, facing the north. Only five people sit to the left of Mia. Jen sits third to the left of Oji. Oji is not an immediate neighbour of Mia. Kia sits to the immediate right of Nia. Ian sits fourth to the right of Jen. Who sits at the extreme right end of the row?
    A Lex Correct Answer Incorrect Answer
    B Kia Correct Answer Incorrect Answer
    C Oji Correct Answer Incorrect Answer
    D Ian Correct Answer Incorrect Answer

    Solution

    Since only five people sit to the left of Mia, Mia must be sitting at the 2nd place from the right. Since Oji is not an immediate neighbor of Mia, Oji must not be sitting either at the extreme right end or at the 3rd place from the right. Since Ian sits fourth to Jen, two cases are possible as shown below. Jen sits third to the left of Oji. This statement is violated in case-2, so it is eliminated. Moving ahead with Case-1. Kia sits to the immediate right of Nia. Lex, the only person left will occupy the vacant position. 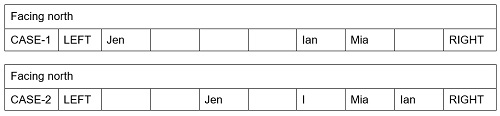  Final arrangement is shown below: It is clear that, Lex sits at the extreme right end of the row. Hence, the correct answer is (A).

    Practice Next
    More Seating Arrangement Questions

    Relevant for Exams:

    ask-question