📢 Too many exams? Don’t know which one suits you best? Book Your Free Expert 👉 call Now!

    âš¡ Month End Offer - Flat 52% Off On All Courses! Enroll Now âš¡
    00:00:00 AM Left

    Question

    Six people, J, K, L, M, N, and O, went to Chennai, on

    different days from Sunday to Friday, of the same week of February, 2024. How many persons went to Pune after K? Statement I: K went three days after J. Only one person went between K and N. N went after K. L went after O. M went before O. Statement II: Two persons went between M and L. Neither M nor L was the first and the last person to visit Pune. O went two days before L. N did not went on Wednesday. K went after J. The question given below consists of two statements I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read all the statements and give answer.
    A Data in statement I alone is sufficient to answer the question and data in statement II alone is not sufficient to answer the question. Correct Answer Incorrect Answer
    B Data in statement II alone is not sufficient to answer the question and data in statement I alone is sufficient to answer the question. Correct Answer Incorrect Answer
    C Data in statement I and statement II together is necessary to answer the question Correct Answer Incorrect Answer
    D Data in both statement I alone and statement II alone is sufficient to answer the question. Correct Answer Incorrect Answer
    E Data neither in statement I alone nor in statement II alone is sufficient to answer the question. Correct Answer Incorrect Answer

    Solution

    From statement I, K went three days after J. Only one person went between K and N. N went after K. L went after O. M went before O. 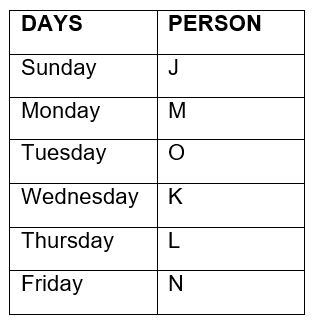Two persons went after K. From statement II, Two persons went between M and L. Neither M nor L was the first and the last person to visit Pune. O went two days before L. N did not went on Wednesday. K went after J. 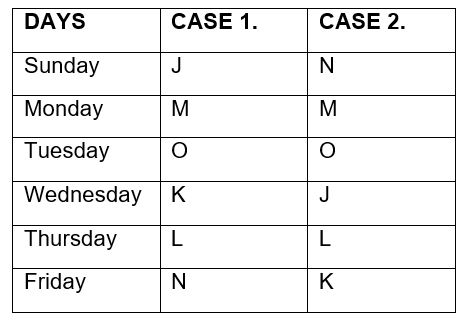Either no person or two persons went after B. So, data in statement I alone is sufficient to answer the question and data in statement II alone is not sufficient to answer the question. 

    Practice Next
    More Data Sufficiency Questions
    ask-question