Question
Out of the eight friends A, B, C, D, E, F, G and H
sitting around a circular table. How many person faces the centre? I. F is immediate neighbor of E but not the neighbor of A. E is not an immediate neighbor of D or C. Three of them are facing the centre. II. The only one who is sitting in between D and F, is not facing the centre. G is third to the right of A and is facing the centre. C is third to the left of D and both are facing the centre. B is the neighbour of F. III. F is an immediate neighbor of B and facing outside. Each of the questions below consists of a question and three statements numbered I, II and III given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read all the three statements and Give answerSolution
From I and II: From II, C is third to the left of D and both are facing the centre. 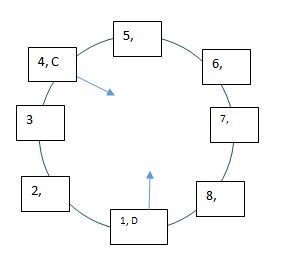 From I, E is not an immediate neighbor of D or C. E can either be seated at 6 or 7.
From I, E is not an immediate neighbor of D or C. E can either be seated at 6 or 7. 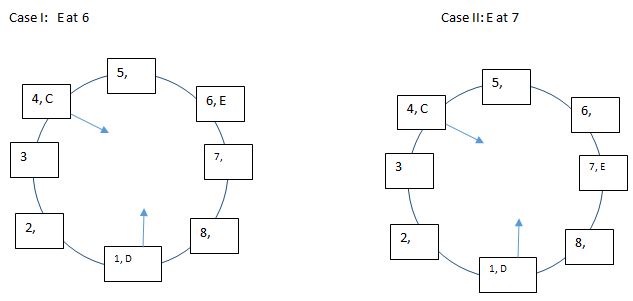 F is an immediate neighbor of E but not of A. And B is the neighbour of F. Thus, in case I, F cannot be seated at 5 because then B cannot be a neighbor of F. Thus F sits at 7 when E sits at 6 and B sits at 8. Similarly, when E is at 7, F cannot be at 8. Thus F sits at 6 when E sits at 7 and B sits at 5. But according to II, The only one who is sitting in between D and F, is not facing the centre. Thus, only person sitting between D and F. Thus, case II discarded.
F is an immediate neighbor of E but not of A. And B is the neighbour of F. Thus, in case I, F cannot be seated at 5 because then B cannot be a neighbor of F. Thus F sits at 7 when E sits at 6 and B sits at 8. Similarly, when E is at 7, F cannot be at 8. Thus F sits at 6 when E sits at 7 and B sits at 5. But according to II, The only one who is sitting in between D and F, is not facing the centre. Thus, only person sitting between D and F. Thus, case II discarded. 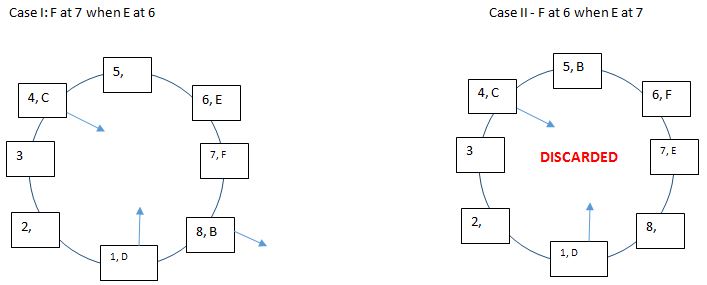 G is third to the right of A and is facing the centre. Also, only three people face the center. Thus A is facing outside.
G is third to the right of A and is facing the centre. Also, only three people face the center. Thus A is facing outside. 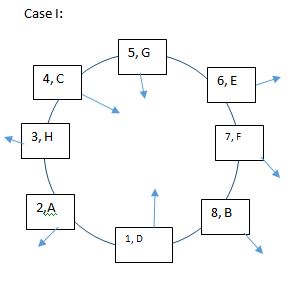
2807, 1400, 697, 346, 171, 84, 41, ?
1, 6, 27, 124, ?, 3906, 27391
...5, 23, 18, 36, 31, ?
124, 128, ?, 135, 110, 146
12, 25, 51, ?, 207, 415
28, 43, 73, 118, ?, 253
37, 49, 63, ?, 97, 117
What will come in place of the question mark (?) in the following series?
24, 8, 15, ?, 12, 4
16.12 × 15.94 + 654.92 – 344.83 = ?× 5.95
What will come in place of the question mark (?) in the following series?
555, 430, ?, -320, -1320, -3320
Relevant for Exams:


