Question
R' invested some money at a compound interest rate of
40% p.a., compounded quarterly. If after 9 months, he received an amount of Rs. 1,99,650, then the sum invested by 'R' is equal to: I. The interest received when Rs. 1,25,000 is invested at S.I of 30% p.a. for 4 years. II. The C.P of an item sold for Rs. 2,40,000 at a profit of 40%. III. The difference between the savings of 'Pawan' and 'Qureshi', whose incomes are Rs. (a + 406320) and Rs. (a + 156320), given that each spends 40% of their respective incomes.Solution
ATQ, Effective rate of interest = 40 ÷ 4 = 10% p.a. And effective time period = (9/12) × 4 = 3 terms We know that for compound interest, Amount = Sum × {1 + (rate of interest/100)} time period Let the sum invested be Rs. 'S' So, 199650 = S X {1 + (10/100)} ³ Or, 199650 = S X (1.1) ³ Or, 199650 = 1.331S So, S = 1,50,000 Therefore, sum invested = Rs. 1,50,000 For I: Interest received = (125000 × 0.3 × 4) = Rs. 1,50,000 Therefore, statement I is true. For II: CP of the item = (240000/1.4) = Rs. 171428.57 Therefore, statement II is false. For III: Difference between savings of 'Pawan' and 'Qureshi' = 0.6 × (a + 406320) - 0.6 × (a + 156320) = 0.6 × (406320 - 156320) = 0.6 × 250000 = Rs. 1,50,000 Therefore, statement III is true.
The length of a cuboid is increased by 20%, its breadth is increased by 15% and its height is decreased by 10%. Find the percentage change in its volume.
The ratio of length to breadth of a rectangle is 5:4, respectively. Perimeter of rectangle is 288 cm. If each side of a square is 25% more than the brea...
There's a cone of height 12cm out of which a smaller cone with the same vertex and vertical axis is cut out. What is the ratio of the volume of the larg...
Area of a rectangle is equal to the total surface area of a hemisphere having volume 4394 cm³ . Find the perimeter of the rectangle if its length is 12...
The volume and height of a cylinder are 2662 cm3 and 7 cm. Find the radius of the cylinder.
A field is 125m long and 15m wide. A tank 10m ×7.5m×6m was dug in it and the earth thus dug out was spread equally on the remaining field. The level o...
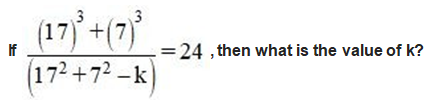
Perimeter of square is 48 cm and length of a rectangle is equal to side of square and breadth of rectangle is 4 cm less than length of the rectangle. F...
The perimeter of a rectangular field is 480 meters and the ratio between the length and breadth is 5:3. The area of the field is:
- Determine the diameter of the incircle of a triangle where the semi-perimeter is 22 cm and the area is 66 cm².
Relevant for Exams:



