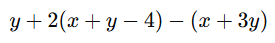📢 Too many exams? Don’t know which one suits you best? Book Your Free Expert 👉 call Now!

    Question

    Two boats A and B are rowing in two different rivers M

    and N respectively. Find the distance covered by boat B in 12 hours downstream. i) Boat A can cover 360 km downstream in 6 hours while B can cover 96 km upstream in 4 hours. ii) Speed of streams (M + N) = 7 km/hr iii) Distance cover by B in y hours downstream is 150 km more than the distance cover by B in (v+5) hours upstream.
    A Only i Correct Answer Incorrect Answer
    B Only i and ii together Correct Answer Incorrect Answer
    C Only i and iii together Correct Answer Incorrect Answer
    D Only i and iii together Correct Answer Incorrect Answer
    E None of these Correct Answer Incorrect Answer

    Solution

    Speed of boat A in still water = VA km/hr Speed of boat B in still water = VB km/hr Speed of river M = m km/hr Speed of river N = n km/hr In 12 hrs boat B will cover 12(VB + n) km From Statement i: VA + m = 60 ------(1) VB + n = 24 ------(2) From statement (ii) m + n = 7 -----(3) From statement iii: One more variable is added as y so we cannot find the answer even combining all the three statements.

    Practice Next
    More Quantity Inequality Questions

    Relevant for Exams:

    ask-question