Question
If four pencils are picked at random, what is the
probability that at least two are of same colour? A box contains 6 red, 4 blue, 2 green and 4 yellow pencils.Solution
Total number of pencils = 6 + 4 + 2 +4 = 16 Let S be the sample space. Then, n(S) = total number of ways of drawing 4 pencils out of 16 = 16C4[if gte msEquation 12]>
If (sin 3A sec 6A = 1) , then what will be the value of cos 6A?
What is the value of cosec30° sec30°?
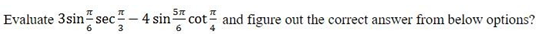
- Determine the value of:(sin 38 o cos 52 o + cos 2 38 o ) X sin 30 o + (cos 60 o tan...
- If 2cosec 2 A – cot 2 A = 5 and 0 o < A < 90 o , then find the value of ‘A’.
Find the maximum value of 14 sin A + 24 cos A.
If sin A - cos A = 3/7, then find value of sinA + cos B, where A is an acute angle.
If 4sin² θ = 3(1+ cos θ), 0° < θ < 90°, then what is the value of (2tan θ + 4sinθ - secθ)?
If tan θ + cot θ = 2 where 0 < θ < 90 ; find the value of tan17 θ + cot19 θ.


