Question
The shadow of a tower standing on level ground is found
to be 40 m longer when the Sun's altitude is 30° than when it was 45°. Find the height (in meters) of the tower.Solution
Let AB be the tower, BC be the shadow at 45°, and BD be the shadow at 30°. The shadow of a tower standing on a level ground is found to be 40 m longer when the sun's altitude is 30° than when it is 45°. i.e. CD = 40 m Let BC = x m In triangle ABC, we have Tan45 =AB/BC AB =x. … (1) In triangle ABD, We have. Tan 30 =AB/BD 1/ √ 3 =AB/x+40 √ 3AB =x+40 X =√ 3AB-40 … (2) x = √ 3x-40 x=40/ (√ 3-1) we multiply the numerator and denominator by the conjugate of the denominator: x=20 (√ 3+1). 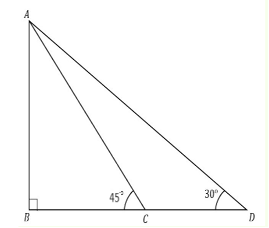
Scrumptious
(i) As science strode scrumptious into one arena of knowledge after another, it discredited claims to the infallibility of revelation...
In the following question, a word has been used in sentences in THREE different ways. Choose the option corresponding to the sentences in which the usa...
Directions: In each question below, word is used in four different ways. Choose the option in which the usage of the word is INCORRECT or INAPPROPRIATE....
Select the most appropriate ANTONYM of the word established from the given sentence:
Siben feels great satisfaction and gratified when he finds...
Guzzle
In the given question, a word has been given and there are three ways in which the word has been used, in similar or different forms. You need to see w...
Issue
I. Politicians proposed popular sovereignty as a means of entrusting the issue to citizens of new territories.
II. I found an old is...
Given below is a word followed by three sentences. You need to understand whether the sentences used the highlighted word correctly or not. Mark the in...
Subtle
(i) The evidence is not detailed enough to subtle his argument.
(ii) The flavour of the dried berries is more subtle .
(iii)...
Directions : A word is given in each question and used in three different sentences. You have to choose the sentence(s) in which the word is used correc...



