📢 Too many exams? Don’t know which one suits you best? Book Your Free Expert 👉 call Now!

    âš¡ Month End Offer - Flat 52% Off On All Courses! Enroll Now âš¡
    00:00:00 AM Left

    Question

    11 people decided to spend an afternoon in two groups. A

    group of them decided to go to the theater and the remaining decided to play tennis. In how many ways can the group for tennis be formed? If there must be at least four people in each group? type-ssc
    A 1584ways Correct Answer Incorrect Answer
    B 1564ways Correct Answer Incorrect Answer
    C 1354ways Correct Answer Incorrect Answer
    D 1786ways Correct Answer Incorrect Answer

    Solution

    Case I- When 4 persons in tennis and rest in the theatre. Number of ways – = 11 C4 × 7 C7 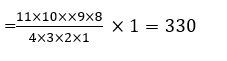Case II- When 5 persons in tennis and rest in theatre number of ways= 11 C5 × 6 C6 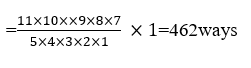Case III-When 6 persons in tennis and rest in theatre= =11C6 × 5 C5   =462 Case IV-When 7 persons in tennis and rest in theatre =11C7 × 4 C4 =330 ways. Total number of ways =2(330+462) =2(792) =1584ways

    Practice Next
    More Permutation and combination Questions

    Relevant for Exams:

    ask-question