Question
How many 4-digit numbers greater than 3000 can be formed
using the digits 1, 2, 3, 4, 5 without repetition?Solution
We must form 4-digit numbers with digits from {1,2,3,4,5}, no repetition, and number > 3000. Thousands digit can be 3, 4, or 5 (3 choices). For each choice of thousands digit, we need to choose and arrange 3 more digits from the remaining 4 digits. Number of ways for remaining 3 places = P(4, 3) = 4 × 3 × 2 = 24. Total number of such 4-digit numbers = 3 × 24 = 72.
In the bar graph, what is the ratio of the average of the to...
The bar graph given below shows the production of sugar (in lakh tonnes) by two different companies P and Q for the given years.
What is the total number of loans which were unsanctioned by all the branches together?
The average speed of a car traveling from city X to city Y is 60 km/h. On its return trip from city Y to city X, due to traffic, the car’s average spe...
Total number of HP laptops sold in 2015 and 2016 together is approximately what percent more of the total number of HP laptops sold in 2017 and 2018 tog...

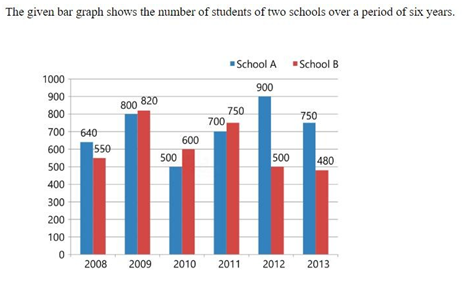
In the bar graph, in which year is the sum of the students f...
The bar graph given below shows the production of paper (in lakh tonnes) by two different companies L and M for the given years.
In 2012, no. of students appearing for IMS was 5%. However each year no of students increases by 10% in number. What will be the difference between the ...
H and V commenced a business with investments of Rs. (p+20000) and Rs. (p-20000), respectively. In the 8th month, H withdrew Rs. 40000 from the business...
Relevant for Exams:



