Question
The volume of a right circular cylinder is given as
64π√3 cm³. The radius of the cylinder's base is 4 cm. Determine the slant height of the cylinder.ÂSolution
Let the height of the cylinder be 'h' cm. Volume of cylinder = (Area of base X height of cylinder) ÷ 3 Area of base = π X (4)2 = 16π cm2 64π√3 = (16π) X h ÷ 3 Or, h = 4√3 Slant height of a cylinder = √(radius2 + height2) = √(16 + 48) = 8 cm
More Mensuration Questions
- Simplify the following trigonometric expression:
15 cos 27° sec 63° − 9 cot 61° tan 29° If √3 tan 2θ – 3 = 0, then find the value of tanθ secθ – cosθ where 0 < θ < 90°
If (cos A - sin A) = √2 cos (90° - A), then find the value of cot A.
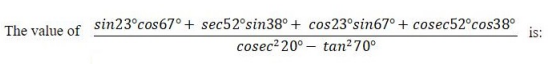
If tan 3.5θ x tan 6.5θ = 1 then the value of tan 5θ is
Find the maximum value of 14 sin A + 24 cos A.
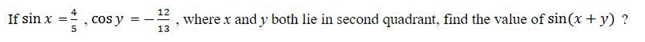
- If cos θ = (4x² – 1)/(1 + 4x²) then find the value of sin q.
The minimum value of 9 cos2 θ + 36 sec2 θ isÂ
Relevant for Exams:
