Question
Ramesh spends 40% of his income and divides the
remaining income among his wife and children (a daughter and a son) in the ratio of 3:4, respectively. If the ratio of the amount received by his daughter to that by his son is 4:3. Find the money spent by Ramesh if his son gets Rs. 3,600.Solution
ATQ, Let the income of Ramesh be Rs. '100c'. Money spent by Ramesh = 0.4 × 100c = Rs. '40c' Money received by his wife = (3/7) × (100c - 40c) = Rs. '30c' Money received by his children = (4/7) × (100c - 40c) = Rs. '60c' Money received by his son = (3/4) × 60c = Rs. '45c' ATQ, 45c = 3600 Or, 'c' = 80 Therefore, money spent by Ramesh = Rs. '40c' = Rs. (40 × 80) = Rs. 3,200

Select an appropriate figure from the four options that would complete the figure.
Find which one word cannot be formed from the given letters of the word.
‘ MANIFEST ’
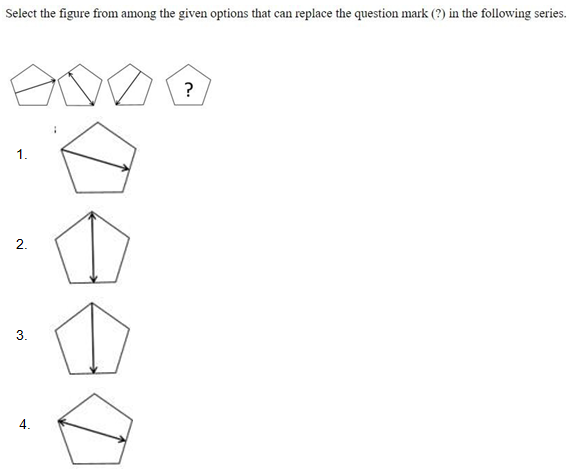
...Select the figure from among the given options that can replace the question mark (?) in the following series.

Read the given statements and conclusions carefully. Assuming that the information given in the statements is true, even if it appears to be at varianc...
Which figure is the correct representation of the movement of food in phloem?
Select the figure series that will replace the question mark [?] in the following figure series.
Identify the figure given in the option which when put in place of the question mark(?) will logically complete the series?
Relevant for Exams:



