Question
There is a 12 m tall hoarding pole on the top of a building. A person at some distance from the building, observes that the angle of elevation to the top of the hoarding pole from that point is the same as the angle of elevation to the bottom of the hoarding pole if he moves 4 √ 3 m closer to the building. What is the angle of elevation that the person is seeing?
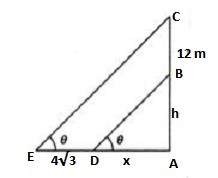Let AB be the building of height ‘h’ and BC be the hoarding pole of height 12 m. Let θ be the angle of elevation as seen by the person at a distance of ‘x’ m and ‘x + 4 √ 3‘ m. In Δ DAB, tan θ = h/x (i) In Δ EAC, tan θ = (h + 12)/ (x + 4 √ 3) (ii) From (i) and (ii) h/x = (h + 12)/ (x + 4 √ 3) ⇒ hx + 4 √ 3h = hx +12x ⇒ h/x = 12/ 4 √ 3 = √ 3 ⇒ tan θ = h/x = √ 3 = tan 60° ⇒ θ = 60°More Height and Distance Questions
- Two men are on opposite sides of a tower of 75 m height. If they measure the elevation of the top of the tower as 30deg; and 45deg; respectively then the d...
- The shadow of a pole 24m long is 56m. Then what will be the approximate shadow of building 40m high at the similar situation?
- The two buildings are 100m apart. From the top of the first building, which is 60m tall, the angle of depression to the top of the second building is 45 de...
- Two buildings are collinear with the base of a tower and are at a distance 9m and 16m from the base of the tower. The angles of elevation from these two bu...
- There are two houses of the same height on both sides of a 30-meter wide road. From a point on the road, elevation angles of the houses are 30° and 60&...
- A pole 21 m high casts a shadow 7√3 m long on the ground. Find the angle of elevation
- A long metallic cable is stretched from a point P on the ground to the top of a cliff, forming an angle of 30 ° with the horizontal ground. The total lengt...
- From a point on the ground, the angle of elevation of the top of a tower is 30°. After moving 20 m closer to the tower in a straight line, the angle of ele...
- A tree of height 'h' meters is partially bent at a certain point above the ground, causing its top to touch the ground at a distance of 12 meters from its ...
- In the village of Hazelton, there was a totem pole 50 m high of which the lower 24 m was carved. According to a clue the treasure was hidden at a point on ...
Relevant for Exams:
Hey! Ask a query
Please enter email id
The email must be a valid email address.
Please enter Mobile Number
Please enter valid Mobile Number
Please enter your Doubt
