Question
The distance between two parallel poles is 65√3 m.
The angle of depression of the top of the second pole when seen from the top of first pole is 30°. What will be the height of second pole if the first pole is 110 m long?Solution
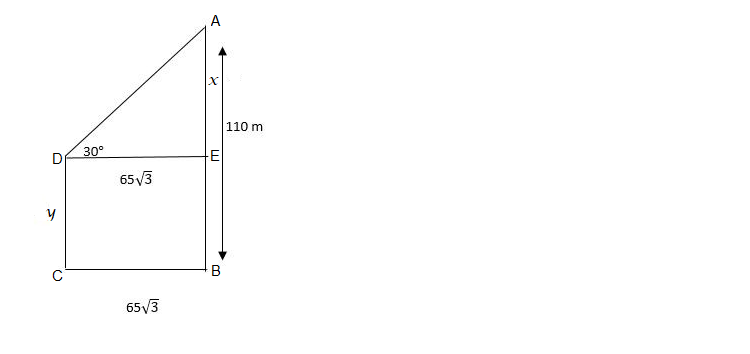Let y be the height of second pole In △ AED, Tan 30° = AE/DE 1/√3 = x/65√3 x = (65√3)/√3 x = 65 therefore, height of the second pole = CD = EB = y y = AB - AE y = 110 – 65 = 45 m
Dinyar Contractor who recently passed away was related to which profession?
The SI number of electrical resistivity is-
Who has recently been appointed as the Defence Secretary of India?
Kuroshio current flows in which of the following oceans?
Which russian banks open special Vostro account with UCO Bank in India?
Eight chairs are placed at a uniform distance from each other around a round table. C and D are equal distance away from both A and B; E sits between A...
In which group are the non-metal elements placed in a vertical column on the right side of the periodic table?
In the National Cooperative Development Corporation (NCDC) was established for strengthening the cooperative activities in
One of the following player is not in the list of Arjuna Awards 2015:
What is the age limit to enter into Deen Dayal Upadhyaya Grameen Kaushalya Yojana?
Relevant for Exams:
