Question
Length of a chord in a circle of radius 'r' cm, is 16 cm
and distance between chord and centre of the circle is 15 cm. Find the value of (5r - 19).Solution
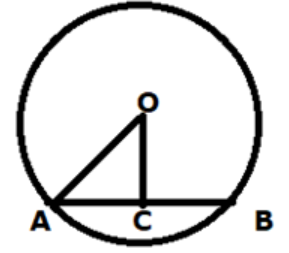
AB is the chord of circle.
Perpendicular line joining the centre of circle and chord, bisects the chord.
i.e. AC = BC = (16/2) = 8 cm
By Pythagoras theorem,
OA 2 = OC 2 + AC 2
Or, r 2 = 15 2 + 8 2
Or, r 2 = 225 + 64
Or, r 2 = 289
So, 'r' = 17
But length cannot be negative. So, 'r' = 17
Required value = 5 X 17 - 19 = 66
(√ 121 x 41) + (3√343 x √289 ) = ? x 19

7, 8, 12, 21, 37, ?
Evaluate: 72 ÷ 6 × (5 + 1) − 8² + 10
What will come in the place of question mark (?) in the given expression?
(30 × 5 + 20) × 2 = ?
What will come in the place of question mark (?) in the given expression?
737 + 149 - ?²- 367 = 14 X 25(√ 1444 ÷ 5) × 3.25 = ?
522 + 160% of 80 - 130 = ? X 13
54% of 250 = 6 × 21 + √?
300% of (3341 – 471) = ? × (√4225/195)
Relevant for Exams:



