Question
AB is parallel to DC in a trapezium ABCD. It is given
that AB > DC and the diagonals AC and BD intersect at O. If AO=3x-15, OB = x +9, OC =x-5 and OD = 5, and x has two values x1 and x2, then the value of (x12 + x2 2 ) is:Solution
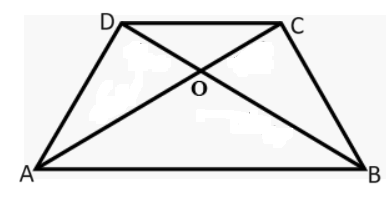Given the trapezium with AB || DC and the diagonals intersecting at O: OD/OB =OC/OA 3x-15/x+9 =x-5/ 5 (3x-15)5 =(x+9) ×(x-5) 15x-75 =x² + 4x – 45 x² -11x + 30 = Solve the quadratic equation: x1 = -6, x2 =-5 x1 = 6, X2 =5 Now- (x12 + x2 2 ) = 36 + 25 = 61
If money is neutral,
What was the primary reason for the reduction in India's current account deficit from USD 67 billion in 2022-23 to USD 23.2 billion in 2023-24?
Keynes assumed that the price level was fixed because
According to the Quantity Theory of Money (QTM), what is the predicted effect of a change in the velocity of money on the price level in the long run?
Real Wages = 500, Consumer price index = 1.2. Calculate nominal wages?
In the Solow model, what is the effect of an increase in the saving rate on the long-term growth rate of an economy?
Locus point of Isoquants wherein the marginal productivity of one of the factors is 0 is called
A card is drawn randomly from a deck of ordinary playing cards. You win Rs.100 if the card is a spade or an ace. What is the probability that you will w...
What is the Cash Reserve Ratio (CRR)?
The inverse demand function for a commodity is P = 50-2Q-Q2 . Calculate the consumer surplus when quantity demanded is 5 unts.
Relevant for Exams:
