Question
If a + b + c = 0 then the value of (1/(a+b)(b+c)) +
(1/(b+c)(c+a)) + (1/(c+a)(a+b)) isSolution
If a + b + c = 0 that means a + b = - c b + c = - a a + C = -b (1 / (a+b)(b+c)) + (1 / (b+c)(c+a)) + (1 / (c+a)(a+b)) Now put the value of equation 1, 2, 3 we get => 1 / (-c × -a) + 1 / (-a × -b) + 1 / (-b × -c) => (1 / ac) + (1 / ab) + (1 / bc) = (b + c + a) / (abc) Also we know that a + b + c = 0 So => (0 / abc) = 0
The Public Sector Insurance companies in India include:
_________ indicates the level of development of insurance sector in a country.
The Insurance Regulatory and Development Authority (IRDAI) was formed on the recommendation of which committee?
Insurance companies can have a exposure of to financial and insurance activities upto ____ of investment assets as per IRDAI.Â
Identify the correct full form of GAAT?
A form of whole-life insurance with a predefined number of premiums to be paid is known as?
What are physical hazards in underwriting?
If a policy holder stops paying the premium after three years, but does not withdraw the money from his policy, then the policy is said to be?
The operative clause in an insurance policy is also known as:
Which among the following is not an element of active listening?Â
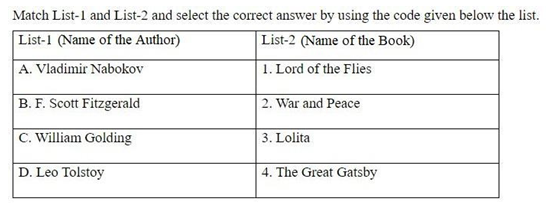
Relevant for Exams:
