Question
The question consists of two statements numbered “I
and II” given below it. You have to decide whether the data provided in the statements are suicient to answer the question. There is a three-digit number represented as ‘xyz’, where z = 4. Find the number ‘xyz’. Statement I: The number ‘xyz’ is divisible by both 7 and 12. Statement II: The sum of digits ‘x’ and ‘y’ is equal to 5.Solution
ATQ, Statement I: Since the number is divisible by 12 and 7, it must be a multiple of (12 × 7) = 84. The numbers satisfying this condition are 504 and 924. Therefore, the data in Statement I alone is not sufficient to answer the question. Statement II: The sum of ‘x’ and ‘y’ is 5. Hence, the data in Statement II alone is not sufficient to answer the question. Combining Statements I and II: The number ‘xyz’ is 504. Thus, the data in both statements together is necessary to answer the question.
The substitution effect for a commodity is
For which of the following consumption functions, the value of income multiplier, k=4?
In the case of cost-push inflation, other things being equal:
Under a flexible exchange rate regime, an expansionary monetary policy will most likely lead to:
Consider the following demand curve Q=100-P in a Duopoly where in A firm is the leader and the B firm is the follower. The Marginal cost given as 20. W...
In an open economy, ceteris paribus, If the marginal propensity to import increases, what will be the impact on Income Multiplier?
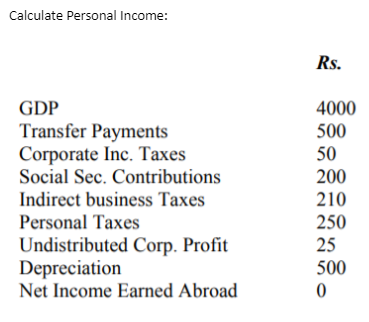
GNP exceeds NNP by:
The measures taken to improve the negative Balance of Payments include ___________.
Which of the following is true for Disposable Income?
Relevant for Exams:



