📢 Too many exams? Don’t know which one suits you best? Book Your Free Expert 👉 call Now!

    Question

    AB is the diameter of a circle centered at O. A tangent

    drawn at point C intersects the extension of AB at point D. If ∠CAB = 38°, find the value of ∠CDB.
    A 128° Correct Answer Incorrect Answer
    B 112° Correct Answer Incorrect Answer
    C 102° Correct Answer Incorrect Answer
    D 132° Correct Answer Incorrect Answer

    Solution

    ATQ,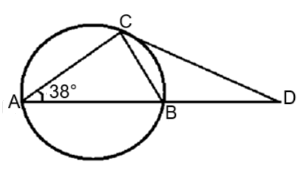

    Image

    Angle made by the diameter of a circle on the arc of the circle is 90°, i.e. ∠ACB = 90°.

    Sum of all angles in a triangle is 180°.

    So, ∠CAB + ∠CBA + ∠ACB = 180°

    Or, 38° + ∠CBA + 90° = 180°

    Or, ∠CBA = 180° - 128°

    Or, ∠CBA = 52°

    Now, ∠CBA + ∠CDB = 180°

    (Linear pair of angles)

    So, ∠CDB = 180 - 52 = 128°

    Practice Next
    More Circle Questions

    Relevant for Exams:

    ask-question