Question
There are three persons 'Amit', 'Bhuvan' and 'Cheetan'
such that 7 times the present age of 'Amit' is equal to 9 times the present age of 'Bhuvan' while 5 times the present age of 'Bhuvan' is equal 3 times the present age of 'Cheetan'. If the present ages of all three are integers and the age of 'Dheeraj' after 13 years will be equal to the sum of the minimum possible present ages of 'Amit', 'Bhuvan' and 'Cheetan', together, then find the present age of 'Dheeraj'.Solution
Let the present ages of 'Amit', 'Bhuvan' and 'Cheetan' be 'x' years, 'y' years and 'z' years respectively According to the question, 7x = 9y Or, x:y = 9:7 = 27:21 Also, 5y = 3z Or, y:z = 3:5 = 21:35 Let 'x' and 'y' be 27a and 21a, respectively Therefore, 'z' = 21a X (35/21) = 35a Therefore, x:y:z = 27:21:35 Therefore, age of 'Dheeraj' 13 years hence from now = 27 + 21 + 35 = 83 years Therefore, required age = 83 - 13 = 70 years
47.87% of 749.76 + 35.11% of 399.76 = √? + 23.15 × 20.87
- What approximate value will come in place of the question mark (?) in the following question? (Note: You are not expected to calculate the exact value.)
(?)2 = (5.99)2 + (7.88)2 + 43.99
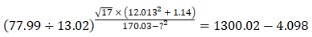
Train 'P' travels at a speed of 45 km/h and crosses train 'Q' in 15 seconds while moving in opposite directions. Determine the speed of train 'Q' if the...
`[(7.99)^2 - (13.001)^2 + (4.01)^3]^2=` ?
A number is first increased by 35% and then decreased by 35%. If the net change in the number is 302.5, then find the original number.
A bag contains red, green, and blue balls, with a total of 16 balls. The probability of drawing two blue balls in one draw is 3/8. How many blue balls a...
35.05% of 14.87 × (13.02 – ?) + 30.19 = 188.7
What approximate value will come in place of the question mark (?) in the following question? (Note: You are not expected to calculate the exact value.)...


